Explanation
1.2 Euclid’s Division Lemma
Consider the following folk puzzle*.
A trader was moving along a road selling eggs. An idler who didn’t have much work to do, started to get the trader into a wordy duel. This grew into a fight, he pulled the basket with eggs and dashed it on the floor. The eggs broke. The trader requested the Panchayat to ask the idler to pay for the broken eggs. The Panchayat asked the trader how many eggs were broken. He gave the following response:
If counted in pairs, one will remain;
If counted in pairs, one will remain. It translates to a = 2u + 1, for some natural number u.
If counted in threes, two will remain;
If counted in threes, two will remain. It translates to a = 3t + 2, for some natural number t.
If counted in fours, three will remain;
If counted in fours, three will remain. It translates to a = 4s + 3, for some natural number s.
If counted in fives, four will remain;
If counted in fives, four will remain. It translates to a = 5w + 4, for some natural number w.
If counted in sixes, five will remain;
If counted in sixes, a = 6q+5, for some natural number q.
If counted in sevens, nothing will remain;
If counted in sevens, nothing will remain, which translates to a = 7p + 0, for some natural number p.
My basket cannot accomodate more than 150 eggs.
That is, in each case, we have a and a positive integer b (in our example, b takes values 7, 6, 5, 4, 3 and 2, respectively) which divides a and leaves a remainder r (in our case, r is 0, 5, 4, 3, 2 and 1, respectively), that is smaller than b. The
This is modified form of a puzzle given in ‘Numeracy Counts!’ by A. Rampal, and others.
Getting back to our puzzle, do you have any idea how you will solve it? Yes! You must look for the multiples of 7 which satisfy all the conditions. By trial and error (using the concept of LCM), you will find he had 119 eggs.
In order to get a feel for what Euclid’s division lemma is, consider the following pairs of integers:
17, 6; 5, 12; 20, 4
Like we did in the example, we can write the following relations for each such pair:
17 = 6 × 2 + 5 (6 goes into 17 twice and leaves a remainder 5)
5 = 12 × 0 + 5 (This relation holds since 12 is larger than 5)
20 = 4 × 5 + 0 (Here 4 goes into 20 five-times and leaves no remainder)
That is, for each pair of positive integers a and b, we have found whole numbers q and r, satisfying the relation:
a = bq + r, 0 ≤ r < b
Note that q or r can also be zero.
Theorem 1.1: (Euclid’s Division Lemma) : Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r < b.
This result was perhaps known for a long time, but was first recorded in Book VII of Euclid’s Elements. Euclid’s division algorithm is based on this lemma.
Euclid’s division algorithm is a technique to compute the Highest Common Factor (HCF) of two given positive integers. Recall that the HCF of two positive integers a and b is the largest positive integer d that divides both a and b.
Let us see how the algorithm works, through an example first. Suppose we need to find the HCF of the integers 455 and 42. We start with the larger integer, that is, 455. Then we use Euclid’s lemma to get
455 = 42 × 10 + 35
Now consider the divisor 42 and the remainder 35, and apply the division lemma to get
42 = 35 × 1 + 7
Now consider the divisor 35 and the remainder 7, and apply the division lemma to get
35 = 7 × 5 + 0
So, let us state Euclid’s division algorithm clearly.
To obtain the HCF of two positive integers, say c and d, with c > d, follow the steps below:
Step 1 : Apply Euclid’s division lemma, to c and d. So, we find whole numbers, q and r such that c = dq + r, 0 ≤ r < d.
Step 2 : If r = 0, d is the HCF of c and d. If r ≠ 0, apply the division lemma to d and r.
Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
This algorithm works because HCF (c, d) = HCF (d, r) where the symbol HCF (c, d) denotes the HCF of c and d, etc.
Example 1 : Use Euclid’s algorithm to find the HCF of 4052 and 12576.
Solution :
Step 1 : Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Step 2 : Since the remainder 420 ≠ 0, we apply the division lemma to 4052 and 420, to get
4052 = 420 × 9 + 272
Step 3 : We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get 272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get 148 = 124 × 1 + 24
We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get 124 = 24 × 5 + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + 0
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.
Notice that 4 = HCF (24, 4) = HCF (124, 24) = HCF (148, 124) = HCF (272, 148) = HCF (420, 272) = HCF (4052, 420) = HCF (12576, 4052).
Euclid’s division algorithm is not only useful for calculating the HCF of very large numbers, but also because it is one of the earliest examples of an algorithm that a computer had been programmed to carry out.
Example 2 : Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer.
Solution : Let a be any positive integer and b = 2. Then, by Euclid’s algorithm, a = 2q + r, for some integer q ≥ 0, and r = 0 or r = 1, because 0 ≤ r < 2. So, a = 2q or 2q + 1.
If a is of the form 2q, then a is an even integer. Also, a positive integer can be either even or odd. Therefore, any positive odd integer is of the form 2q + 1.
Example 3 : Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.
Solution : Let us start with taking a, where a is a positive odd integer. We apply the division algorithm with a and b = 4.
Since 0 ≤ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or 4q + 3, where q is the quotient. However, since a is odd, a cannot be 4q or 4q + 2 (since they are both divisible by 2).
Therefore, any odd integer is of the form 4q + 1 or 4q + 3.
Example 4 : A sweetseller has 420 kaju barfi’s and 130 badam barfi’s. She wants to stack them in such a way that each stack has the same number, and they take up the least area of the tray. What is the number of that can be placed in each stack for this purpose?
Solution : This can be done by trial and error. But to do it systematically, we find HCF (420, 130). Then this number will give the maximum number of barfi’s in each stack and the number of stacks will then be the least. The area of the tray that is used up will be the least.
Now, let us use Euclid’s algorithm to find their HCF. We have :
420 = 130 × 3 + 30
130 = 30 × 4 + 10
30 = 10 × 3 + 0
So, the HCF of 420 and 130 is 10.
Therefore, the sweetseller can make stacks of 10 for both kinds of barfi.
1.3The Fundamental Theorem of Arithmetic
any natural number can be written as a product of its prime factors. For instance, 2 = 2, 4 = 2 × 2, 253 = 11 × 23, and so on. Now, let us try and look at natural numbers from the other direction. That is, can any natural number be obtained by multiplying prime numbers? Let us see.
Take any collection of prime numbers, say 2, 3, 7, 11 and 23. If we multiply some or all of these numbers, allowing them to repeat as many times as we wish, we can produce a large collection of positive integers (In fact, infinitely many). Let us list a few :
7 × 11 × 23 = 1771 3 × 7 × 11 × 23 = 5313
2 × 3 × 7 × 11 × 23 = 10626 23 × 3 × 73 = 8232
22 × 3 × 7 × 11 × 23 = 21252
We are going to use the factor tree with which you are all familiar. Let us take some large number, say, 32760, and factorise it as shown :
So we have factorised 32760 as 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 as a product of primes, i.e., 32760 = 23 × 32 × 5 × 7 × 13 as a product of powers of primes. Let us try another number, say, 123456789. This can be written as 32 × 3803 × 3607. Of course, you have to check that 3803 and 3607 are primes!
This leads us to a conjecture that every composite number can be written as the product of powers of primes. In fact, this statement is true, and is called the Fundamental Theorem of Arithmetic.
Theorem 1.2 : (Fundamental Theorem of Arithmetic) : Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.
The Fundamental Theorem of Arithmetic says that every composite number can be factorised as a product of primes. Actually it says more. It says that given any composite number it can be factorised as a product of prime numbers in a ‘unique’ way, except for the order in which the primes occur. So, for example, we regard 2 × 3 × 5 × 7 as the same as 3 × 5 × 7 × 2, or any other possible order in which these primes are written. This fact is also stated in the following form:
The prime factorisation of a natural number is unique, except for the order of its factors. In general, given a composite number x, we factorise it as x = $$p_{1}p_{2} ... p_{n}$$, where $$p_{1}, p_{2},..., p_{n}$$ are primes and written in ascending order, i.e., $$p_{1} ≤ p_{2} ≤ . . . ≤ p_{n}$$. If we combine the same primes, we will get powers of primes. For example, 32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 × 32 × 5 × 7 × 13
Once we have decided that the order will be ascending, then the way the number is factorised, is unique.
The Fundamental Theorem of Arithmetic has many applications, both within mathematics and in other fields. Let us look at some examples.
Example 5 : Consider the numbers $$4^{n}$$, where n is a natural number. Check whether there is any value of n for which $$4^{n}$$ ends with the digit zero.
Solution : If the number $$4^{n}$$, for any n, were to end with the digit zero, then it would be divisible by 5. That is, the prime factorisation of 4n would contain the prime 5. This is
not possible because $$4^{n}$$ = $$(2)^{2n}$$; so the only prime in the factorisation of 4n is 2. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of $$4^{n}$$. So, there is no natural number n for which 4n ends with the digit zero.
How to find the HCF and LCM of two positive integers using the Fundamental Theorem of Arithmetic in earlier classes, without realising it! This method is also called the prime factorisation method. Let us recall this method through an example.
Example 6 : Find the LCM and HCF of 6 and 20 by the prime factorisation method.
Solution : We have : 6 = $$2^{1} × 3^{1}$$ and 20 = 2 × 2 × 5 = $$2^{2} × 5^{1}$$.
You can find HCF(6, 20) = 2 and LCM(6, 20) = 2 × 2 × 3 × 5 = 60, as done in your earlier classes.
Note that HCF(6, 20) = $$2^{1}$$ = Product of the smallest power of each common prime factor in the numbers.
LCM (6, 20) = $$2^{2} × 3^{1} × 5^{1}$$ =Product of the greatest power of each prime factor, involved in the numbers.
From the example above, you might have noticed that HCF(6, 20) × LCM(6, 20) = 6 × 20. In fact, we can verify that for any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b. We can use this result to find the LCM of two positive integers, if we have already found the HCF of the two positive integers.
Example 7 : Find the HCF of 96 and 404 by the prime factorisation method. Hence, find their LCM.
Solution : The prime factorisation of 96 and 404 gives :
96 = $$2^{5}$$ × 3, 404 = $$2^{2}$$ × 101
Therefore, the HCF of these two integers is $$2^{2}$$ = 4.
Also, LCM (96, 404) = $$\frac{96 X 404}{HCF(96, 404)} = \frac{96 X 404}{4}$$ = 9696
Example 8 : Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.
Solution : We have : 6 = 2 × 3, 72 = $$2^{3} × 3^{2}$$, 120 = $$2^{3}$$ × 3 × 5
Here, $$2^{1}$$ and $$3^{1}$$ are the smallest powers of the common factors 2 and 3, respectively.
So, HCF (6, 72, 120) = $$2^{1} × 3^{1}$$ = 2 × 3 = 6
$$2^{3}, 3^{2}$$ and $$5^{1}$$ are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers.
So, LCM (6, 72, 120) = 23 × 32 × 51 = 360
1.4 Revisiting Irrational Numbers
Introduced to irrational numbers and many of their properties. You studied about their existence and how the rationals and the irrationals together made up the real numbers. You even studied how to locate irrationals on the number line. However, we did not prove that they were irrationals. In this section, we will prove that $$\sqrt{2}, \sqrt{3}, \sqrt{5}$$ and, in general, $$\sqrt{q}$$ is irrational, where p is a prime. One of the theorems, we use in our proof, is the Fundamental Theorem of Arithmetic.
Theorem 1.3 : Let p be a prime number. If p divides $$a^{2}$$, then p divides a, where a is a positive integer.
Proof : Let the prime factorisation of a be as follows :
a = $$pˍ{1} p_{2} . . . p_{n}$$, where $$p_{1},p_{2}, . . ., p_{n}$$ are primes, not necessarily distinct. Therefore, $$a^{2} = ( p_{1} p_{2} . . . p_{n}) ( p_{1} p_{2} . . . p_{n})$$ = $$p_{1}^{2}p_{2}^{2} . . . p_{2}^{n}$$.
Now, we are given that p divides $$a^{2}$$. Therefore, from the Fundamental Theorem of Arithmetic, it follows that p is one of the prime factors of $$a^{2}$$. However, using the uniqueness part of the Fundamental Theorem of Arithmetic, we realise that the only prime factors of $$a^{2}$$ are $$p_{1}, p_{2}, . . ., p_{n}$$. So p is one of $$p_{1}, p_{2}, . . ., p_{n}$$.
Now, since a = $$p_{1} p_{2} . . . p_{n}$$, p divides a.
We are now ready to give a proof that $$\sqrt{2}$$ is irrational.
The proof is based on a technique called ‘proof by contradiction’. (This technique is discussed in some detail in Appendix 1).
Theorem 1.4: $$\sqrt{2}$$ is irrational.
Proof : Let us assume, to the contrary, that $$\sqrt{2}$$ is rational.
So, we can find integers r and s (≠ 0) such that $$\sqrt{2} = \frac{r}{s}$$.
Suppose r and s have a common factor other than 1. Then, we divide by the common
factor to get , $$\sqrt{2} = \frac{a}{b}$$ = where a and b are coprime.
So, $$b\sqrt{2}$$= a.
Squaring on both sides and rearranging, we get $$2b^{2} = a^{2}$$. Therefore, 2 divides $$a^{2}$$.
Now, by Theorem 1.3, it follows that 2 divides a.
So, we can write a = 2c for some integer c.
Substituting for a, we get $$2b^{2} = 4c^{2}$$, that is, $$b^{2} = 2c^{2}$$.
This means that 2 divides $$b^{2}$$, and so 2 divides b (again using Theorem 1.3 with p = 2).
Therefore, a and b have at least 2 as a common factor.
But this contradicts the fact that a and b have no common factors other than 1.
This contradiction has arisen because of our incorrect assumption that $$\sqrt{2}$$ is rational.
So, we conclude that $$\sqrt{2}$$ is irrational.
Example 9 : Prove that $$\sqrt{3}$$ is irrational.
Solution : Let us assume, to the contrary, that $$\sqrt{3}$$ is rational.
That is, we can find integers a and b (≠ 0) such that $$\sqrt{3} = \frac{a}{b}$$.
Suppose a and b have a common factor other than 1, then we can divide by the common factor, and assume that a and b are coprime.
So, $$b\sqrt{3}$$ = a.
Squaring on both sides, and rearranging, we get $$3b^{2} = a^{2}$$.
Therefore, $$a^{2}$$ is divisible by 3, and by Theorem 1.3, it follows that a is also divisible by 3.
So, we can write a = 3c for some integer c.
Substituting for a, we get $$3b^{2} = 9c^{2}$$, that is, $$b^{2} = 3c^{2}$$.
This means that $$b^{2}$$ is divisible by 3, and so b is also divisible by 3 (using Theorem 1.3 with p = 3).
Therefore, a and b have at least 3 as a common factor.
But this contradicts the fact that a and b are coprime.
This contradiction has arisen because of our incorrect assumption that $$\sqrt{3}$$ is rational. So, we conclude that $$\sqrt{3}$$ is irrational.
Example 10 : Show that $$5 - \sqrt{3}$$ is irrational.
Solution : Let us assume, to the contrary, that $$5 – \sqrt{3}$$ is rational.
That is, we can find coprime a and b (b ≠ 0) such that $$5 - \sqrt{3} = \frac{a}{b}$$.
Therefore, $$5 - \frac{a}{b}$$ = \sqrt{3}$$
Rearranging this equation, we get $$\sqrt{3} = 5 - \frac{a}{b} = \frac{5b - a}{b}$$.
Since a and b are integers, we get $$5 – \frac{a}{b}$$ is rational, and so $$\sqrt{3}$$ is rational.
But this contradicts the fact that $$\sqrt{3}$$ is irrational.
This contradiction has arisen because of our incorrect assumption that $$5 – \sqrt{3}$$ is rational.
So, we conclude that $$5 - \sqrt{3}$$ is irrational.
Example 11 : Show that $$3\sqrt{2}$$ is irrational.
Solution : Let us assume, to the contrary, that $$3\sqrt{2}$$ is rational.
That is, we can find coprime a and b (b ≠ 0) such that $$3 \sqrt{2} = \frac{a}{b}$$
Rearranging, we get $$\sqrt{2} = \frac{a}{3b}$$.
Since 3, a and b are integers, $$\frac{a}{3b}$$ is rational, and so $$\sqrt{2}$$ is rational.
But this contradicts the fact that $$\sqrt{2}$$ is irrational.
So, we conclude that $$3\sqrt{2}$$ is irrational.
1.5Revisiting Rational Numbers and Their Decimal Expansions
The rational numbers have either a terminating decimal expansion or a non-terminating repeating decimal expansion. In this section, we are going to consider a rational number, say $$\frac{p}{q}$$ (q ≠ 0), and explore exactly when the decimal expansion of $$\frac{p}{q}$$ is terminating and when it is non-terminating repeating (or recurring). We do so by considering several examples.
Let us consider the following rational numbers :
(i)0.375 (ii)0.104 (iii)0.0875 (iv)23.3408.
Now (i)0.375 = $$\frac{375}{1000} = \frac{375}{10^{3}}$$
ii)0.104 = $$\frac{104}{1000} = \frac{104}{10^{3}}$$
iii)0.0875 = $$\frac{875}{10000} = \frac{875}{10^{4}}$$
iv)23.3408 = $$\frac{233408}{10000} = \frac{233408}{10^{4}}$$
As one would expect, they can all be expressed as rational numbers whose denominators are powers of 10. Let us try and cancel the common factors between the numerator and denominator and see what we get :
i)0.375 = $$\frac{375}{10^{3}} = \frac{3 X 5^{3}}{2^{3} X 5^{3}} = \frac{3}{2^{3}}$$
ii)0.104 = $$\frac{104}{10^{3}} = \frac{13 X 2^{3}}{2^{3} X 5^{3}} = \frac{13}{5^{3}}$$
iii)0.0875 = $$\frac{875}{10^{4}} = \frac{7}{2^{4} X 5}$$
iv)23.3408 = $$\frac{233408}{10^{4}} = \frac{2^{2} X 7 X 521}{5^{4}}$$
Theorem 1.5 : Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form , $$\frac{a}{b}$$ where p and q are coprime, and the prime factorisation of q is of the form $$2^{n}5^{m}$$, where n, m are non-negative integers.
You are probably wondering what happens the other way round in Theorem 1.5. That is, if we have a rational number of the form , $$\frac{p}{q}$$, and the prime factorisation of q is of the form $$2^{n}5^{m}$$, where n, m are non negative integers, then does $$\frac{p}{q}$$ have a terminating decimal expansion?
Let us see if there is some obvious reason why this is true. You will surely agree that any rational number of the form , $$\frac{a}{b}$$ where b is a power of 10, will have a terminating decimal expansion. So it seems to make sense to convert a rational number of the form $$\frac{a}{b}$$, where q is of the form $$2^{n}5^{m}$$, to an equivalent rational number of the form $$\frac{a}{b}$$, where b is a power of 10. Let us go back to our examples above and work backwards.
i)$$\frac{3}{8} = \frac{3}{2^{3}} = \frac{3 X 5^{3}}{2^{3} x 5^{3}} = \frac{375}{10^{3}}$$ = 0.375
ii)$$\frac{13}{125} = \frac{13}{5^{3}} = \frac{13 X 2^{3}}{2^{3} X 5^{3}} = \frac{104}{10^{3}}$$ = 0.104
iii)$$\frac{7}{80} = \frac{7}{2^{4} X 5} = \frac{7 X 5^{3}}{2^{4} X 5^{4}} = \frac{875}{10^{4}}$$ = 0.0875
iv)$$\frac{14588}{625} = \frac{2^{2} X 7 X 521}{5^{4}} = \frac{2^{6} X 7 X 521}{2^{4} X 5^{4}} = \frac{233408}{10^{4}}$$ = 23.3408
So, these examples show us how we can convert a rational number of the form $$\frac{p}{q}$$, where q is of the form $$2^{n}5^{5}$$, to an equivalent rational number of the form $$\frac{a}{b}, where b is a power of 10. Therefore, the decimal expansion of such a rational number terminates. Let us write down our result formally.
Theorem 1.6 : Let x = $$\frac{p}{q}$$ be a rational number, such that the prime factorisation of q is of the form $$2^{n}5^{m}$$, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
We are now ready to move on to the rational numbers whose decimal expansions are non-terminating and recurring. Once again, let us look at an example to see what is going on.
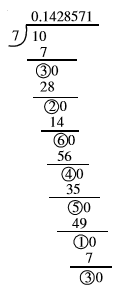Here, remainders are 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, 1, . . . and divisor is 7.
Notice that the denominator here, i.e., 7 is clearly not of the form 2n5 m. Therefore, from Theorems 1.5 and 1.6, we know that $$\frac{1}{7}$$ will not have a terminating decimal expansion.
Hence, 0 will not show up as a remainder (Why?), and the remainders will start repeating after a certain stage. So, we will have a block of digits, namely, 142857, repeating in the quotient $$\frac{1}{7}$$.
Theorem 1.7: Let x = $$\frac{p}{q}$$, where p and q are coprimes, be a rational number, such that the prime factorisation of q is not of the form $$2^{n}5^{m}$$, where n, m are non-negative integers. Then, x has a decimal expansion which is non-terminating repeating (recurring) .
From the discussion above, we can conclude that the decimal expansion of every rational number is either terminating or non-terminating repeating.
0 Doubts's