2.2Geometrical Meaning of the Zeroes of a Polynomial

You know that a real number k is a zero of the polynomial p(x) if p(k) = 0. But why are the zeroes of a polynomial so important? To answer this, first we will see the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.

Consider first a linear polynomial ax + b, a ≠ 0. You have studied in Class IX that the graph of y = ax + b is a straight line. For example, the graph of y = 2x + 3 is a straight line passing through the points (– 2, –1) and (2, 7).

X	-2	2
Y = 2x + 3	-1	7

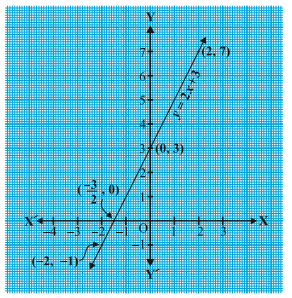
The graph of y = 2x + 3 intersects the x-axis mid-way between x = –1 and x = – 2,

that is, at the point (-3/2, 0). You also know that the zero of 2x + 3 is -3/2. Thus, the zero of the polynomial 2x + 3 is the x – coordinate of the point point where the graph of y = 2x + 3 intersects the x-axis.

In general, for a linear polynomial ax + b, a ≠ 0, the graph of y = ax + b is a straight line which intersects the x-axis at exactly one point, namely, (-b/a, 0).

Therefore, the linear polynomial ax + b, a ≠ 0, has exactly one zero, namely, the x-coordinate of the point where the graph of y = ax + b intersects the x-axis.

Now, let us look for the geometrical meaning of a zero of a quadratic polynomial. Consider the quadratic polynomial x2 – 3x – 4. Let us see what the graph* of y = x2 – 3x – 4 looks like. Let us list  a few values of y = x2 – 3x – 4 corresponding to a few values for x.

X	-2	-1	0	1	2	3	4	5
Y = $$x^{2}$$ - 3x - 4	6	0	-4	-6	-6	-4	0	6

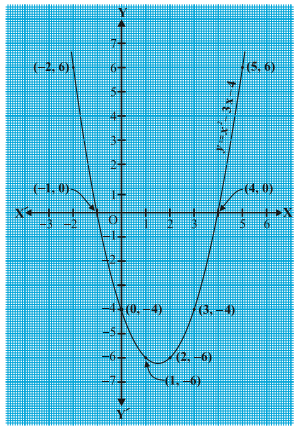
In fact, for any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like  or open

downwards like  depending on whether a > 0 or a < 0.

Also note from Fig. 2.2 that –1 and 4 are the x-coordinates of the points where the graph of y = x2 –3x – 4 intersects the x-axis. Thus, the zeroes of the quadratic polynomial x 2 – 3x – 4 are x-coordinates of the points where the graph of y = x 2 – 3x – 4 intersects the x -axis.

Case (i) : Here, the graph cuts x-axis at two distinct points A and A′.

The x-coordinates of A and A′ are the two zeroes of the quadratic polynomial $$ax^{2}$$ + bx + c

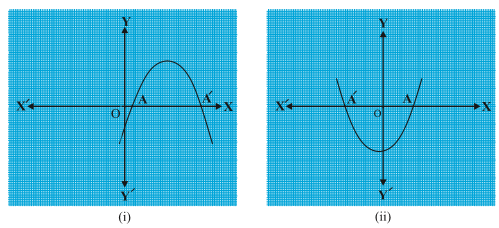
Case (ii) : Here, the graph cuts the x-axis at exactly one point, i.e., at two coincident points. So, the two points A and A′ of Case (i) coincide here to become one point A.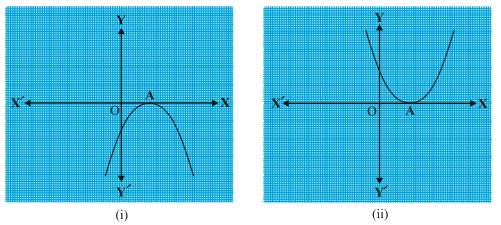

Case (iii) : Here, the graph is either completely above the x-axis or completely below the x-axis. So, it does not cut the x-axis at any point.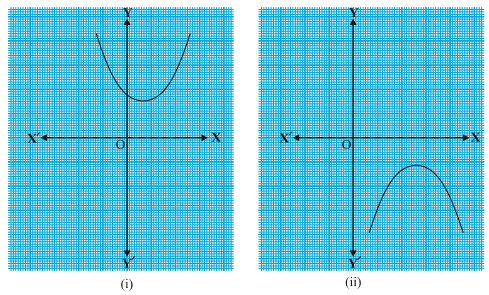

So, the quadratic polynomial $$ax^{2}$$ + bx + c has no zero in this case.

So, you can see geometrically that a quadratic polynomial can have either two distinct zeroes or two equal zeroes (i.e., one zero), or no zero. This also means that a polynomial of degree 2 has atmost two zeroes.

Now, what do you expect the geometrical meaning of the zeroes of a cubic polynomial to be? Let us find out. Consider the cubic polynomial $$x^{3}$$ – 4x. To see what the graph of y = $$x^{3}$$ – 4x looks like, let us list a few values of y corresponding to a few values for x.

X	-2	-1	0	1	2
Y = $$x^{3}$$ - 4x	0	3	0	-3	0

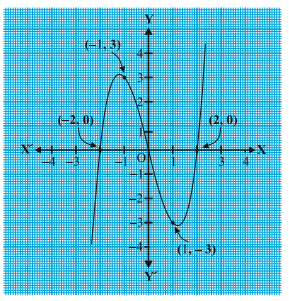
Locating the points of the table on a graph paper and drawing the graph, we see that the graph of y = $$x^{3}$$ – 4x

We see from the table above that – 2, 0 and 2 are zeroes of the cubic polynomial x3 – 4x. Observe that –2, 0 and 2 are, in fact, the x-coordinates of the only points where the graph of y = $$x^{3}$$ – 4x intersects the x-axis. Since the curve meets the x-axis in only these 3 points, their x-coordinates are the only zeroes of the polynomial

Let us take a few more examples. Consider the cubic polynomials $$x^{3}$$ and $$x^{3} – x^{2}$$. We draw the graphs of y = $$x^{3}$$ and y = $$x^{3} – x^{2}$$

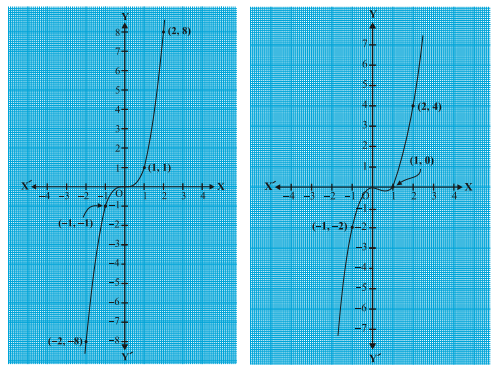
Note that 0 is the only zero of the polynomial $$x^{3}$$. Also, can see that 0 is the x-coordinate of the only point where the graph of y = $$x^{3}$$ intersects the x-axis. Similarly, since $$x^{3} – x^{2} = x^{2}$$ (x – 1),  0 and 1 are the only zeroes of the polynomial $$x^{3} – x^{2}$$. Also, from these values are the x-coordinates of the only points where the graph of y = $$x^{3} – x^{2}$$ intersects the x-axis.

Example 1 : Look at the graphs. Each is the graph of y = p(x), where p(x) is a polynomial. For each of the graphs, find the number of zeroes of p(x).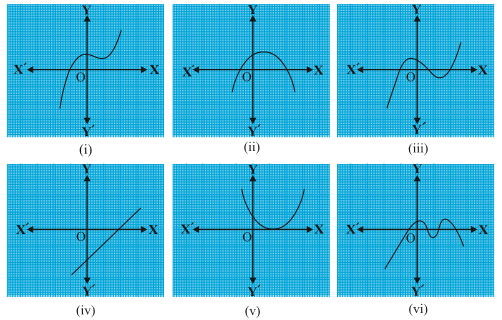

(i)The number of zeroes is 1 as the graph intersects the x-axis at one point only.

(ii)The number of zeroes is 2 as the graph intersects the x-axis at two points.

(iii)The number of zeroes is 3.

(iv)The number of zeroes is 1.

(v)The number of zeroes is 1.

(vi)The number of zeroes is 4.

2.3 Relationship between Zeroes and Coefficients of a Polynomial

You have already seen that zero of a linear polynomial ax + b is $$\frac{b}{a}$$ . We will now try to answer the question raised in Section 2.1 regarding the relationship between zeroes and coefficients of a quadratic polynomial. For this, let us take a quadratic polynomial, say p(x) = $$2x^{2}$$ – 8x + 6.Factorise quadratic polynomials by splitting the middle term. So, here we need to split the middle term ‘– 8x’ as a sum of two terms, whose product is 6 × $$2x^{2} = 12x^{2}$$. So, we write

$$2x^{2}$$ – 8x + 6 = $$2x^{2}$$ – 6x – 2x + 6 = 2x(x – 3) – 2(x – 3)

= (2x – 2)(x – 3) = 2(x – 1)(x – 3)

Example 2 : Find the zeroes of the quadratic polynomial x 2 + 7x + 10, and verify the relationship between the zeroes and the coefficients.

Solution : We have

$$x^{2}$$ + 7x + 10 = (x + 2)(x + 5)

So, the value of $$x^{2}$$ + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0, i.e., when x = – 2 or x = –5. Therefore, the zeroes of $$x^{2}$$ + 7x + 10 are – 2 and – 5. Now,

Sum of zeroes = -2 + (-5) = -(7) = $$\frac{-(7)}{1} = \frac{-coefficient \:\: of \:\: x}{coefficient \:\: of \:\: x^{2}}$$

Product of zeroes = (-2) X (-5) = 10 = $$\frac{10}{1} = \frac{constant \:\: term}{coefficient \:\: of \:\: x^{2}}$$

Example 3 : Find the zeroes of the polynomial $$x^{2}$$ – 3 and verify the relationship between the zeroes and the coefficients.

Solution : Recall the identity $$a^{2} – b^{2}$$ = (a – b)(a + b). Using it, we can write:

$$x^{2} – 3 = (X - \sqrt{3}) (X + \sqrt{3})$$

So, the value of $$x^{2}$$ - 3 is zero when X = $$\sqrt{3}$$ or $$X = -\sqrt{3}$$.

Therefore, the zeroes of $$x^{2} – 3$$ are $$\sqrt{3}$$ and $$-\sqrt{3}$$.

Now,

Sum of zeroes = $$\sqrt{3} - \sqrt{3} = 0 = \frac{-(coefficient \:\: of \:\: x)}{coefficient \:\: of \:\: x^{2}}$$,

Product of zeroes = $$(\sqrt{3})(-\sqrt{-3} = -3 = \frac{-3}{1} = \frac{constant \:\: term}{coefficient \:\: of \:\: x^{2}}$$.

Example 4 : Find a quadratic polynomial, the sum and product of whose zeroes are –3 and 2, respectively.

Solution : Let the quadratic polynomial be $$ax^{2} + bx + c$$, and its zeroes be α and β. We have

α + β = – 3 = $$\frac{-b}{a}$$,

and αβ = 2 = $$\frac{c}{a}$$.

If a = 1, then b = 3 and c = 2.

So, one quadratic polynomial which fits the given conditions is $$x^{2}$$ + 3x + 2.

You can check that any other quadratic polynomial that fits these conditions will be of the form $$k(x^{2} + 3x + 2)$$, where k is real.

Let us now look at cubic polynomials. Do you think a similar relation holds between the zeroes of a cubic polynomial and its coefficients? Let us consider p(x) = $$2x^{3} – 5x^{2}$$ – 14x + 8.

You can check that p(x) = 0 for x = 4, – 2, $$\frac{1}{2}$$. Since p(x) can have atmost three

zeroes, these are the zeroes of $$2x^{3} – 5x^{2} – 14x + 8$$. Now,

sum of the zeroes = 4 + (-2) + $$\frac{1}{2} = \frac{5}{2} = \frac{-(-5)}{2} = \frac{-(coefficient \:\: of \:\: x^{2})}{coefficient \:\: of \:\: x^{3}}$$,

product of the zeroes = 4 X (-2) X $$\frac{1}{2} = -4 = \frac{-8}{2} = \frac{-constant \:\: term}{coefficient \:\: of \:\: x^{3}}$$

However, there is one more relationship here. Consider the sum of the products of the zeroes taken two at a time. We have

$${4 X (-2)} + {(-2) X \frac{1}{2}} + {\frac{1}{2} X 4}$$

= -8 – 1 + 2 = -7 = $$\frac{-14}{2} = \frac{coefficient \:\: of \:\: x}{coefficient \:\: of \:\: x^{3}}$$.

In general, it can be proved that if α, β, γ are the zeroes of the cubic polynomial $$ax^{3} + bx^{2} + cx + d$$, then

α + β + γ = $$\frac{-b}{a}$$,

αβ + βγ + γα = $$\frac{c}{a}$$,

α β γ = $$\frac{-d}{a}$$.

Let us consider an example.

Example 5* : Verify that 3, –1, $$-\frac{1}{3}$$ are the zeroes of the cubic polynomial p(x) = $$3x^{3} – 5x^{2} – 11x – 3$$, and then verify the relationship between the zeroes and the coefficients.

Solution : Comparing the given polynomial with $$ax^{3} + bx^{2} + cx + d$$, we get

a = 3, b = – 5, c = –11, d = – 3. Further

p(3) = $$3 × 3^{3} – (5 × 3^{2})$$ – (11 × 3) – 3 = 81 – 45 – 33 – 3 = 0,

p(–1) = $$3 × (–1)^{3} – 5 × (–1)^{2} – 11 × (–1) – 3$$ = –3 – 5 + 11 – 3 = 0,

$$p(\frac{-1}{3}) = 3 X (-\frac{1}{3})^{3} – 5 X (-\frac{1}{3})^{2} – 11 X (-\frac{1}{3}) – 3$$,

= $$(-\frac{1}{9} - \frac{5}{9} + \frac{11}{3} – 3 = - \frac{2}{3} + \frac{2}{3}$$ = 0

Therefore, 3, - 1 and $$-\frac{1}{3}$$ are the zeroes of $$3x^{3} – 5x^{2}$$ – 11x – 3.

So, we take α = 3, β = -1 and γ = $$\frac{1}{3}$$.

α + β + γ = 3 + (-1) + $$(-\frac{1}{3}) = 2 - \frac{1}{3} = \frac{5}{3} = \frac{-(-5)}{3} = \frac{-b}{a}$$,

αβ + βγ + γα =3 x (-1) + (-1) X $$(-\frac{1}{3}) + (-\frac{1}{3}) x 3 = -3 + \frac{1}{3} – 1 = \frac{-11}{3} = \frac{c}{a}$$

αβγ = 3 x (-1) X $$(-\frac{1}{3}) = 1 = \frac{-(-3)}{3} = \frac{-d}{a}$$.

2.4 Division Algorithm for Polynomials

You know that a cubic polynomial has at most three zeroes. However, if you are given only one zero, can you find the other two? For this, let us consider the cubic polynomial $$x^{3} – 3x^{2} – x + 3$$. If we tell you that one of its zeroes is 1, then you know that x – 1 is a factor of $$x^{3} – 3x^{2}$$ – x + 3. So, you can divide $$x^{3} – 3x^{2}$$ – x + 3 by x – 1, as to get the quotient $$x^{2}$$ – 2x – 3.

Next, you could get the factors of $$x^{2}$$ – 2x – 3, by splitting the middle term, as (x + 1)(x – 3). This would give you

$$x^{3} – 3x^{2}$$ – x + 3 = (x – 1)($$x^{2}$$ – 2x – 3)

= (x – 1)(x + 1)(x – 3)

So, all the three zeroes of the cubic polynomial are now known to you as 1, – 1, 3.

Example 6 : Divide $$2x^{2}$$ + 3x + 1 by x + 2.

Solution : Note that we stop the division process when either the remainder is zero or its degree is less than the degree of the divisor. So, here the quotient is 2x – 1 and the remainder is 3. Also,

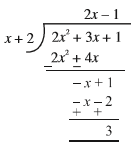
(2x – 1)(x + 2) + 3 = $$2x^{2} + 3x – 2 + 3 = 2x^{2}$$ + 3x + 1 i.e., $$2x^{2}$$ + 3x + 1 = (x + 2)(2x – 1) + 3

Therefore, Dividend = Divisor × Quotient + Remainder

Let us now extend this process to divide a polynomial by a quadratic polynomial.

Example 7 : Divide $$3x^{3} + x^{2}$$ + 2x + 5 by 1 + 2x + $$x^{2}$$.

Solution : We first arrange the terms of the dividend and the divisor in the decreasing order of their degrees. Recall that arranging the terms in this order is called writing the polynomials in standard form. In this example, the dividend is already in standard form, and the divisor, in standard form, is $$x^{2} + 2x + 1$$.

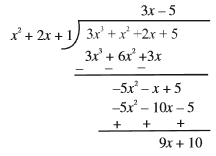
Step 1 : To obtain the first term of the quotient, divide the highest degree term of the dividend (i.e., $$3x^{3}$$) by the highest degree term of the divisor (i.e., $$x^{2}$$). This is 3x. Then carry out the division process. What remains is $$– 5x^{2} – x + 5$$.

Step 2 : Now, to obtain the second term of the quotient, divide the highest degree term of the new dividend (i.e., $$–5x^{2}$$) by the highest degree term of the divisor (i.e., $$x^{2}$$). This gives –5. Again carry out the division process with $$–5x^{2}$$ – x + 5.

Step 3 : What remains is 9x + 10. Now, the degree of 9x + 10 is less than the degree of the divisor $$x^{2}$$ + 2x + 1. So, we cannot continue the division any further.

So, the quotient is 3x – 5 and the remainder is 9x + 10. Also,

($$x^{2}$$ + 2x + 1) × (3x – 5) + (9x + 10) = $$3x^{3} + 6x^{2} + 3x – 5x^{2}$$ – 10x – 5 + 9x + 10

= $$3x^{3} + x^{2}$$ + 2x + 5

Here again, we see that

Dividend = Divisor x Quotient + Remainder

If p(x) and g (x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that

p(x) = g(x) × q(x) + r (x),

where r(x) = 0 or degree of r(x) < degree of g(x).

This result is known as the Division Algorithm for polynomials.

Example 8 : Divide $$3x^{2} – x^{3}$$ – 3x + 5 by x – 1 – $$x^{2}$$, and verify the division algorithm.

Solution : Note that the given polynomials are not in standard form. To carry out division, we first write both the dividend and divisor in decreasing orders of their degrees.

So, dividend = $$–x^{3} + 3x^{2} – 3x + 5$$ and divisor = $$–x^{2} + x – 1$$.

Division process is shown on the right side.

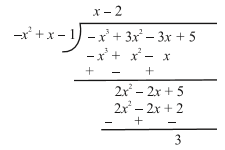
We stop here since degree (3) = 0 < 2 = degree ($$–x^{2}$$ + x – 1).

So, quotient = x – 2, remainder = 3.

Now,

Divisor × Quotient + Remainder

= ($$–x^{2}$$ + x – 1) (x – 2) + 3

= $$–x^{3} + x^{2} – x + 2x^{2} – 2x + 2 + 3$$

= $$–x^{3} + 3x^{2} – 3x + 5$$

= Dividend

Example 9 : Find all the zeroes of $$2x^{4} – 3x^{3} – 3x^{2} + 6x – 2$$, if you know that two of its zeroes are $$\sqrt{2} and $$-\sqrt{2}$$.

Solution : Since two zeroes are $$\sqrt{2}$$ and $$-\sqrt{2}$$, $$(x - \sqrt{2}) (x + \sqrt{2})$$ = $$x^{2} – 2$$ is a factor of the given polynomial.  Now, we divide the given polynomial by  $$x^{2} – 2$$.

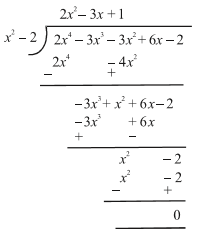
First term of quotient is $$\frac{2x^{4}}{x^{2}} = 2x^{2}$$

Second term of quotient is $$\frac{-3x^{3}}{x^{2}} = -3x$$

Third term of quotient is $$\frac{x^{2}}{x^{2}}$$ = 1

So, $$2x^{4} – 3x^{3} – 3x^{2} + 6x – 2$$ = $$(x^{2} – 2)(2x^{2} – 3x + 1)$$.

Now, by splitting –3x, we factorise $$2x^{2}$$ – 3x + 1 as (2x – 1)(x – 1). So, its zeroes

are given by x = $$\frac{1}{2}$$ and x = 1. Therefore, the zeroes of the given polynomial are

$$\sqrt{2}, -\sqrt{2}, \frac{1}{2}$$, and 1.

Please Login For Further Details...

Submit