- 3.2 Pair of Linear Equations in Two Variables
- Exercise 3.1
- 3.3 Graphical Method of Solution of a Pair of Linear Equations
- Exercise 3.2
- 3.4 Algebraic Methods of Solving a Pair of Linear Equations
- Exercise 3.3
- 3.4.2 Elimination Method
- Exercise 3.4
- 3.4.3 Cross - Multiplication Method
- Exercise 3.5
- 3.5 Equations Reducible to a Pair of Linear Equations in Two Variables
- Exercise 3.6
- Exercise 3.7
3.2 Pair of Linear Equations in Two Variables
3.2 Pair of Linear Equations in Two Variables
linear equations in two variables: 2x + 3y = 5
x – 2y – 3 = 0
and x – 0y = 2, i.e., x = 2
the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables x and y.
For example, let us substitute x = 1 and y = 1 in the left hand side (LHS) of the equation 2x + 3y = 5. Then
LHS = 2(1) + 3(1) = 2 + 3 = 5,
which is equal to the right hand side (RHS) of the equation.
Therefore, x = 1 and y = 1 is a solution of the equation 2x + 3y = 5.
Now let us substitute x = 1 and y = 7 in the equation 2x + 3y = 5. Then,
LHS = 2(1) + 3(7) = 2 + 21 = 23 which is not equal to the RHS.
Therefore, x = 1 and y = 7 is not a solution of the equation.
Geometrically, what does this mean? It means that the point (1, 1) lies on the line representing the equation 2x + 3y = 5, and the point (1, 7) does not lie on it. So, every solution of the equation is a point on the line representing it.
In fact, this is true for any linear equation, that is, each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.
These two linear equations are in the same two variables x and y. Equations like these are called a pair of linear equations in two variables.
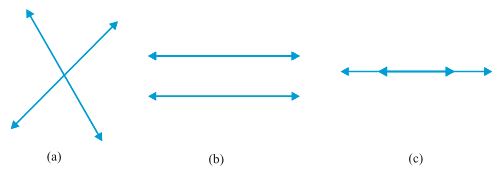
given two lines in a plane, only one of the following three possibilities can happen:
(i) The two lines will intersect at one point.
(ii) The two lines will not intersect, i.e., they are parallel.
(iii) The two lines will be coincident.
We show all these possibilities in Fig.
In Fig. 3.1 (a), they intersect.
In Fig. 3.1 (b), they are parallel.
In Fig. 3.1 (c), they are coincident.
 Example 1 : Let us take the example given in Section 3.1. Akhila goes to a fair with ` 20 and wants to have rides on the Giant Wheel and play Hoopla. Represent this situation algebraically and graphically (geometrically).
Example 1 : Let us take the example given in Section 3.1. Akhila goes to a fair with ` 20 and wants to have rides on the Giant Wheel and play Hoopla. Represent this situation algebraically and graphically (geometrically).
Solution : The pair of equations formed is :
y =1/ 2 x
i.e., x – 2y = 0…………. (1)
3x + 4y = 20 ………………(2)
Let us represent these equations graphically. For this, we need at least two solutions for each equation. We give these solutions in Table
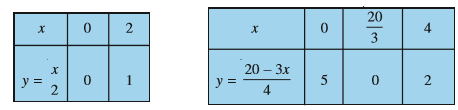 For instance, putting x = 0 in Equation (2), we get 4y = 20, i.e., y = 5. Similarly, putting y = 0 in Equation (2), we get
For instance, putting x = 0 in Equation (2), we get 4y = 20, i.e., y = 5. Similarly, putting y = 0 in Equation (2), we get
3x = 20, i.e.,x=\frac{20}{3}. But \frac{20}{3} is not an integer, it will not be easy to plot exactly on the graph paper. So, we choose y = 2 which gives x = 4, an integral value.
Plot the points A(0, 0), B(2, 1) and P(0, 5), Q(4, 2), corresponding to the solutions in Table 3.1. Now draw the lines AB and PQ, representing the equations x – 2y = 0 and 3x + 4y = 20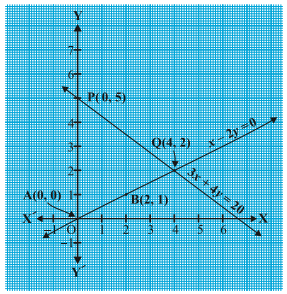 Example 2 : Romila went to a stationery shop and purchased 2 pencils and 3 erasers for ` 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she also bought 4 pencils and 6 erasers of the same kind for ` 18. Represent this situation algebraically and graphically.
Example 2 : Romila went to a stationery shop and purchased 2 pencils and 3 erasers for ` 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she also bought 4 pencils and 6 erasers of the same kind for ` 18. Represent this situation algebraically and graphically.
Solution : Let us denote the cost of 1 pencil by ` x and one eraser by ` y. Then the
algebraic representation is given by the following equations:
2x + 3y = 9………….. (1)
4x + 6y = 18…………. (2)
To obtain the equivalent geometric representation, we find two points on the line representing each equation. That is, we find two solutions of each equation.
These solutions are given below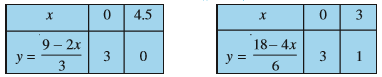
We plot these points in a graph paper and draw the lines. We find that both the lines coincide. This is so, because, both the equations are equivalent, i.e., one can be derived from the other.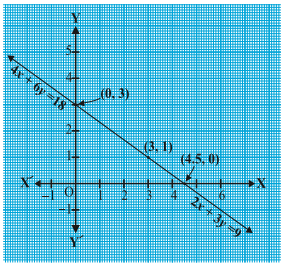
Example 3 : Two rails are represented by the equations x + 2y – 4 = 0 and 2x + 4y – 12 = 0. Represent this situation geometrically.
Solution : Two solutions of each of the equations :
x + 2y – 4 = 0 ……………….(1)
2x + 4y – 12 = 0 …………….(2)
are given in Table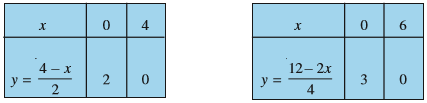
To represent the equations graphically, we plot the points R(0, 2) and S(4, 0), to get the line RS and the points P(0, 3) and Q(6, 0) to get the line PQ.
We observe in Fig. that the lines do not intersect anywhere, i.e., they are parallel.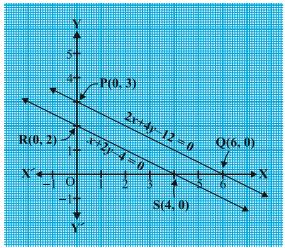



0 Doubts's