Exercise 3.1

1.Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.

Sol.Let the present ages of Aftab and his daughter be x years and y years respectively. Then the algebraic representation of the situation in the above data is given by the following equations:

$$x-7=7(y-7)  \Rightarrow x-7=7y-49$$

$$x+3=3(y+3) \Rightarrow x+3=3y+9$$

$$\Rightarrow    x-7y+42=0$$………….(1)

And    x-3y-6=0……….(2)

to represent these equations graphically. We find two solutions for each equation.

These solutions are given below:

For equation (1)

x-7y+42=0

7y=x+42   $$ \Rightarrow y=\frac{x+42}{7}$$

Table 1 of solutions

(for x=7, $$ y=\frac{7+42}{7}=\frac{49}{7}=7$$)

For equation (2)

$$x-3y-6=0 \Rightarrow 3y=x-6$$

$$y=\frac{x-6}{3}$$

table 2 of solutions

We plot the points A(0, 6)and B(7,7) corresponding  to the solutions 1 on graph paper and join these points by a ruler to get the line AB representing the equation (1).

Also plot the points C(0, -2) and D(6,0)corresponding to the solutions in table 2 on the same graph paper and join these points by a ruler to get the line CD representing the equation (2), as shown in the graph.

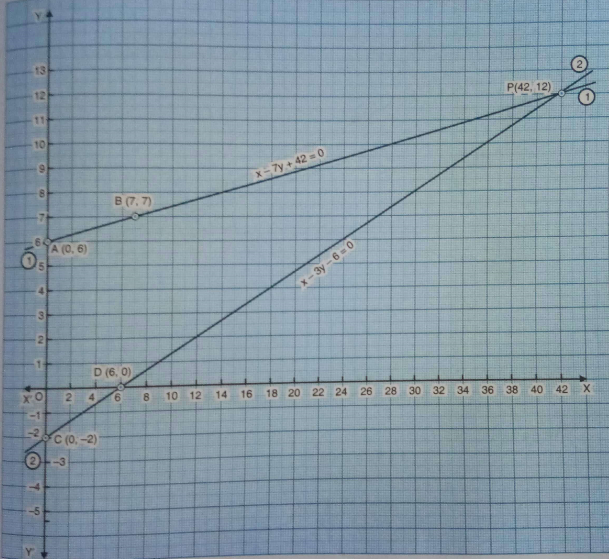We observe from the graph that the two lines representing the two equations are intersecting at the point P(42, 12).

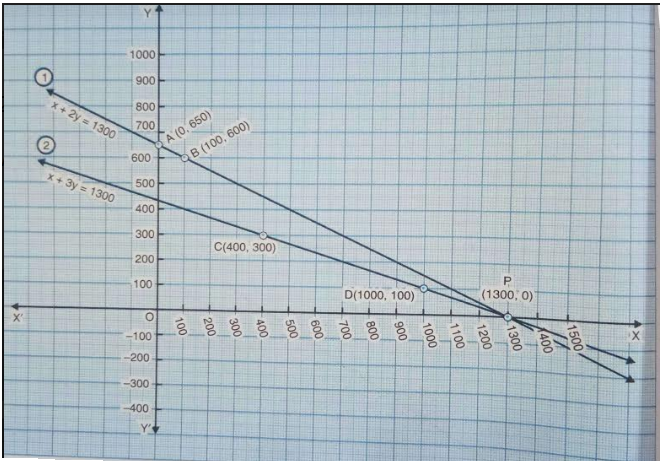
2.The coach of a cricket team buys 3 bats and 6 balls for ` 3900. Later, she buys another bat and 3 more balls of the same kind for ` 1300. Represent this situation algebraically and geometrically.

Sol.Let us denote the cost of one batby rs x and one ball rs y. then the algebraic representation of the situation in the above data is given by the following equations:

3x+6y=3900         Dividing by 3,   x+2y=1300

                  And     x+3y=1300

To represent these equations graphically, we find two solutions for each equation. These solutions are given below:

For equation (1)

x+2y=1300

$$\Rightarrow   2y=1300-x$$

$$\Rightarrow  y=\frac{1300-x}{2}$$

Table 1 of solutions

For equation (2)

X+3y=1300

3y=1300-x

$$Y=\frac{1300-x}{3}$$

Table 2 of solutions

We plot the points A(0, 650) and B(100, 600) corresponding to the solutions in table 1 on a graph paper and join these points by a ruler to get the line AB representing the equation (1).

Also plot the points C(400, 300) and D(1000, 100) corresponding to the solutions in table 2 on the same graph paper and join these points by a ruler to get the line CD representing the equation (2),

We observe in the graph that the two lines representing the two equations are intersecting at the point P(1300, 0)

3.The cost of 2 kg of apples and 1kg of grapes on a day was found to be ` 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ` 300. Represent the situation algebraically and geometrically.

Sol.Let the cost of 1 kg of apples be rs x and of 1 kg of grapes be rs y.

Then, the algebraic representation of the situation in the above data is given by the following equations:

2x+y=160 …………..(1)

4x+2y=300

Dividing by 2,       $$\Rightarrow 2x+y=150$$……………(2)

To represent these equations graphically, we find two solutions for each equation. These solutions are given below:

For equation (1)

2x+y=160

Y=160-2x

Table 1 of solutions

(it may be noted that x=0 has not been put to find y because for x=0, y=160 which is much larger than 60 and 40 but the reader is free to take x=0.)

For equation (2)

2x+y=150

Y=150-2x

Table 2 of solutions

We plot the points A(50, 60) and B(40, 80) corresponding to the solutions in table 1 on a graph paper and join these points by a ruler to get the line AB representing the equation (1).

Also plot the points C(50, 50) and D(30, 90) corresponding to the solutions in table 2, on the same graph paper and join these points by a ruler to get the line CD representing the equation (2) as shown in the graph given below:

We observe from the graph that, the two lines do not intersect anywhere i.e., they are parallel.