Exercise 6.3
Exercise 6.3
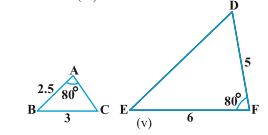
1.State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
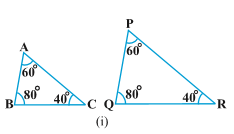
Sol.In $$\Delta ABC$$ and $$\Delta PQR$$,
$$\angle A = \angle P = 60^{\circ}$$
$$\angle B = \angle Q = 80^{\circ}$$
$$\angle C = \angle R = 40^{\circ}$$
$$\therefore \Delta ABC \sim \Delta PQR$$
|AAA similarity criterion
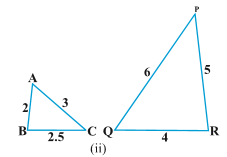
Sol.In $$\Delta ABC$$ and $$\Delta QRP$$,
$$\frac{AB}{QR} = \frac{2}{4} = \frac{1}{2}$$,
$$\frac{BC}{RP} = \frac{2.5}{5} = \frac{25}{50} = \frac{1}{2}$$
And $$\frac{CA}{PQ} = \frac{3}{6} = \frac{1}{2}$$
$$\therefore \frac{AB}{QR} = \frac{BC}{RP} = \frac{CA}{PQ}$$
$$ \Delta ABC$$ is similar to $$\Delta QRP$$ by SSS similarity criterion.
$$\therefore \Delta ABC \sim \Delta PQR$$
Remark. The reader is strongly suggested to observe that:
In the solution of part (ii) and figure given for part (ii), the ratio of corresponding sides is not same but the sides of one triangle are of course in the same ratio to the sides of second triangle.
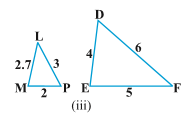
Sol.No; because for $$\Delta MPL$$ and $$\Delta EFD$$, the sides of one triangle are not in the same ratio to the sides of the other triangle.
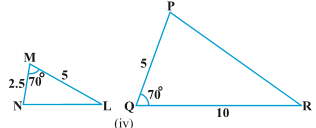
Sol.In $$\Delta MNL$$ and $$\Delta QPR$$
$$\frac{ML}{QR} = \frac{MN}{QP}(= \frac{1}{2})$$
And $$\angle NML = \angle PQR (= 70^{0})$$
$$\therefore \Delta MNL \sim \Delta QPR$$
|SAS similarity criterion
Sol.No
[$$\because$$ In both triangles, one angle is given = $$80^{0}$$ but in $$\Delta ABC$$ only one side containing this angle is given]
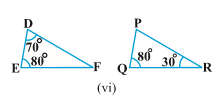
Sol.In $$\Delta DEF$$,
$$\angle F = 180^{0} – (70^{0} + 80^{0})$$
= $$180^{0} – 150^{0} = 30^{0}$$
($$\because$$ Sum of three angles of a triangle is $$180^{0}$$
In $$\Delta PQR$$,
$$\angle P = 180^{0} – (80^{0} + 30^{0})$$
($$\because$$ Sum of three angles of a triangle is $$180^{0}$$)
= $$180^{0} – 110^{0} = 70^{0}$$
Now in $$\Delta DEF$$ and $$\Delta PQR$$,
$$\angle D$$ = $$\angle P(= 70^{0})$$
$$\angle E$$ = $$\angle Q (= 80^{0})$$
$$\angle F$$ = $$\angle R (= 30^{0})$$
$$\therefore \Delta DEF \sim \Delta PQR$$
|AAA similarity criterion
2.In Fig. 6.35, ∆ ODC ~ ∆ OBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB.
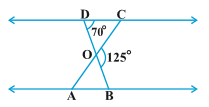
Sol.$$ \angle DOC + \angle BOC = 180^{0}$$
|Linear pair Axiom
$$\Rightarrow \angle DOC + 125^{0} = 180^{0}$$
$$\Rightarrow \angle DOC = 180^{0} – 125^{0}$$
$$\Rightarrow \angle DOC = 55^{0}$$ …..(1)
In $$\Delta DOC, \angle DOC + \angle ODC + \angle DCO = 180^{0}$$
|$$\because$$ The sum of the three angles of a triangle is $$180^{0}$$
$$\Rightarrow 55^{0} + 70^{0} + \angle DCO = 180^{0}$$
$$\Rightarrow 125^{0} + \angle DCO = 180^{0}$$
$$\Rightarrow \angle DCO = 180^{0} – 125^{0}$$
$$\Rightarrow \angle DCO = 55^{0}$$ …… (2)
$$\because \Delta ODC \sim \Delta OBA$$ |Given
$$\therefore \angle OAB = \angle DCO = 55^{0}$$ … (3)
|Corresponding angles of two similar triangles are equal
3.Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $$\frac{OA}{OC} = \frac{OB}{OD}$$.
Sol.Given : Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O.
To prove : $$\frac{OA}{OC} = \frac{OB}{OD}$$
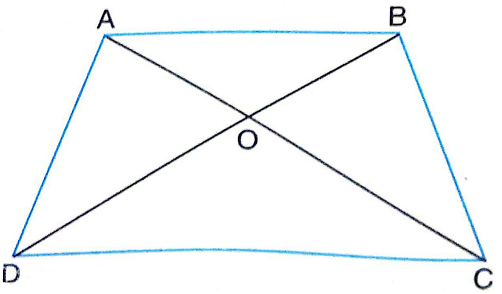
Proof : In $$\Delta OAB$$ and $$\Delta OCD$$,
$$\angle OAB = \angle OCD$$
|Alternate Interior Angles ($$\because$$ AB || DC and AC intersects them)
$$\angle OBA = \angle ODC$$
|Alternate Interior Angles ($$\because$$ AB || DC and BD intersects them)
$$\therefore \Delta OAB \sim \Delta OCD$$
|AA similarity criterion
$$\therefore \frac{OA}{OC} = \frac{OB}{OD}$$
($$\because$$ corresponding sides of two similar triangles are proportional)
4.In fig. 6.36, $$\frac{QR}{QS} = \frac{QT}{PR}$$ and $$\angle 1 = \angle 2$$. Show that $$\Delta PQS \sim \Delta TQR$$.
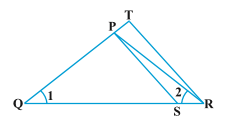
Sol.Given : In figure, $$\frac{QR}{QS} = \frac{QT}{PR}$$ and $$\angle 1 = \angle 2$$.
To Prove : $$\Delta PQS \sim \Delta TQR$$
Proof : In $$\Delta PQR$$,
$$\because \angle 1 = \angle 2$$
$$\therefore$$ PR = QP
|$$\because$$ sides opposite to equal angles of a triangle are equal
Now,
$$\frac{QR}{QS} = \frac{QT}{PR}$$
Putting PR = QP FROM (1),
$$\Rightarrow \frac{QR}{QS} = \frac{QT}{QP}$$
Taking reciprocals,
$$\frac{QS}{QR} = \frac{QP}{QT}$$
Now, in $$\Delta PQS$$ and $$\Delta TQR$$,
$$\frac{QS}{QR} = \frac{QP}{QT}$$
And $$\angle SQP = \angle RQT$$ (= $$\angle 1$$ each)
$$\therefore \Delta PQS \sim \Delta TQR$$
|SAS similarity criterion
5.S and T are points on sides PR and QR of ∆ PQR such that ∠ P = ∠ RTS. Show that ∆ RPQ ~ ∆ RTS.
Sol.Given : S and T are points on sides PR and QR of $$\Delta PQR$$ such that $$\angle P = \angle RTS$$.
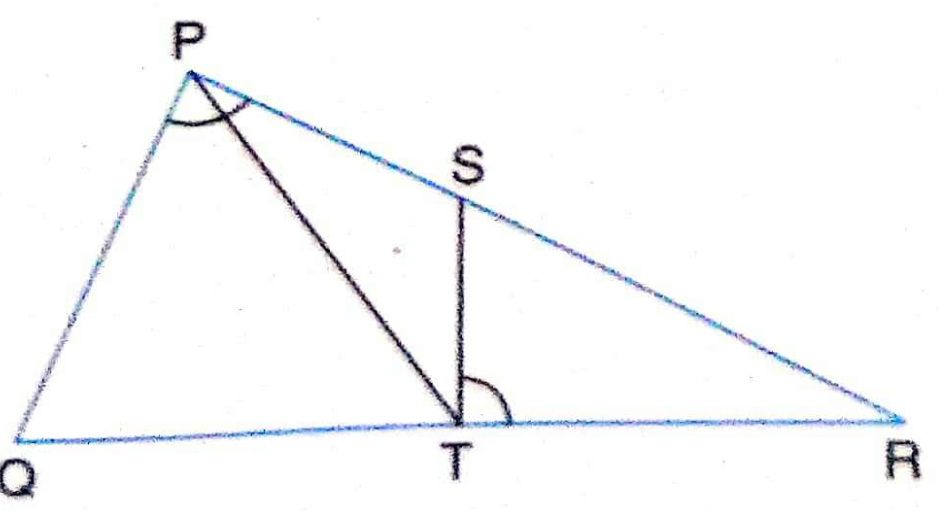
To prove : $$\Delta RPQ \sim \Delta RTS$$
Proof : In $$\Delta RPQ$$ and $$\Delta RTS$$,
$$\angle P$$ i.e., $$\angle RPQ$$ = $$\angle RTS$$ |Given
$$\angle QRP = \angle SRT$$ |common angle
$$\therefore \Delta RPQ \sim \Delta RTS$$
|AA similarity criterion
6.In Fig. 6.37, if ∆ ABE ≅ ∆ ACD, show that ∆ ADE ~ ∆ ABC.
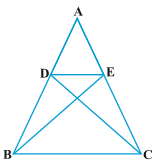
Sol.Given : In figure,
∆ ABE ≅ ∆ ACD.
To prove : ∆ ADE ~ ∆ ABC
Proof :
$$\because$$ ∆ ABE ≅ ∆ ACD |Given
$$\therefore$$ AB = AC …..(1)
And AE = AD
$$\Rightarrow$$ AD = AE …. (2)
Dividing (1) by (2),
$$\therefore \frac{AB}{AD} = \frac{AC}{AE}$$ … (3)
Also, $$\angle DAE = \angle BAC$$ |common $$\angle$$ …. (4)
In view of (3) and (4),
∆ ADE ~ ∆ ABC
|SAS similarity criterion
7.In Fig. 6.38, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i)∆ AEP ~ ∆ CDP
(ii)∆ ABD ~ ∆ CBE
(iii)∆ AEP ~ ∆ ADB
(iv)∆ PDC ~ ∆ BEC
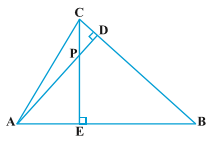
Sol.Given : In figure, altitudes AD and CE of $$\Delta ABC$$ intersect each other at the point P.
To Prove :
(i)∆ AEP ~ ∆ CDP
(ii)∆ ABD ~ ∆ CBE
(iii)∆ AEP ~ ∆ ADB
(iv)∆ PDC ~ ∆ BEC
Proof : (i)In ∆ AEP and ∆ CDP,
$$\angle AEP = \angle CDP$$ … (1)
|By def. of altitude, each equal to $$90^{0}$$
$$\angle EPA = \angle DPC$$ …. (2)
|vert. opp. $$\angle S$$
In view of (1) and (2),
∆ AEP ~ ∆ CDP
|AA similarity criterion
(ii)∆ ABD ~ ∆ CBE
Sol.In ∆ ABD and ∆ CBE,
$$\angle ADB = \angle CEB$$ … (1)
|Echa equal to $$90^{0}$$
$$\angle ABD = \angle CBE$$ …. (2)
|Common angle
In view of (1) and (2),
∆ ABD ~ ∆ CBE
|AA similarity criterion
(iii)∆ AEP ~ ∆ ADB
Sol.In $$\Delta AEP$$ and $$\Delta ADB$$,
$$\angle AEP = \angle ADB$$ …. (1)
|Each equal to $$90^{0}$$
$$\angle EAP = \angle DAB$$
|Common angle
In view of (1) and (2),
∆ AEP ~ ∆ ADB
|AA similarity criterion
(iv)∆ PDC ~ ∆ BEC
Sol.In ∆ PDC and ∆ BEC,
$$\angle PDC = \angle BEC$$ …(1)
|Each equal to $$90^{0}$$
$$\angle DCP = \angle ECB$$ … (2)
|Common angle
In view of (1) and (2),
∆ PDC ~ ∆ BEC
|AA similarity criterion
8.E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ ABE ~ ∆ CFB.
Sol.Given : E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.
To prove : $$\Delta ABE \sim \Delta CFB$$
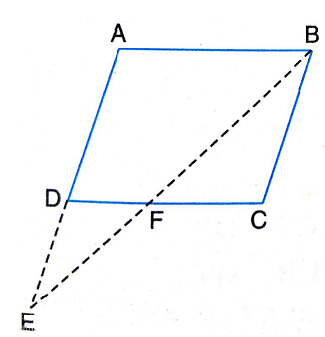
Proof : In $$\Delta ABE$$ and $$\Delta CFB$$,
$$\angle BAE = \angle FCB$$ … (1)
|Opp. $$\angle S$$ of a parallelogram
$$\angle AEB = \angle CBF$$ … (2)
|Alt. Int. $$\angle S$$ ($$\because$$ AE || BC and BE intersects them)
In view of (1) and (2),
$$\Delta ABE \sim \Delta CFB$$.
|AA similarity criterion
9.In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i)∆ ABC ~ ∆ AMP
(ii)$$\frac{CA}{PA} = \frac{BC}{MP}$$
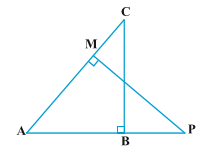
Sol.Given : In figure, ABC and AMP are two right triangles, right angled at B and M respectively.
To prove : i)∆ ABC ~ ∆ AMP
(ii)$$\frac{CA}{PA} = \frac{BC}{MP}$$
Proof : i)∆ ABC ~ ∆ AMP
Sol.In ∆ ABC and ∆ AMP,
$$\angle ABC = \angle AMP$$ … (1)
|Each equal to $$90^{0}$$
$$\angle BAC = \angle MAP$$ … (2)
|Common angle
In view of (1) and (2),
∆ ABC ~ ∆ AMP
|AA similarity criterion
ii)$$\frac{CA}{PA} = \frac{BC}{MP}$$
sol.$$\because$$ ∆ ABC ~ ∆ AMP
|Proved above in (i)
$$\frac{CA}{PA} = \frac{BC}{MP}$$
|corresponding sides of two similar triangles are proportional
10.CD and GH are respectively the bisectors of ∠ ACB and ∠ EGF such that D and H lie on sides AB and FE of ∆ ABC and ∆ EFG respectively. If ∆ ABC ~ ∆ FEG, show that:
i)$$\frac{CD}{GH} = \frac{AC}{FG}$$
(ii)∆ DCB ~ ∆ HGE
(iii)∆ DCA ~ ∆ HGF
Sol.Given : CD and GH are respectively the bisectors of $$\angle ACB$$ and $$\angle EGF$$ such that D and H lie on sides AB and FE of $$\Delta ABC$$ and $$\Delta EFG$$ respectively.
Also, $$\Delta ABC ~ ∆ FEG$$.
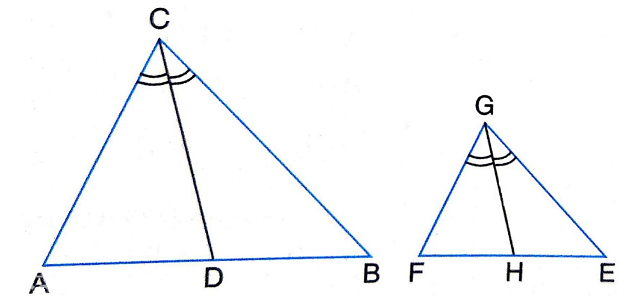
To Prove :
i)$$\frac{CD}{GH} = \frac{AC}{FG}$$
(ii)∆ DCB ~ ∆ HGE
(iii)∆ DCA ~ ∆ HGF
Proof : (i)In ∆ ACD and ∆ FGH,
$$\angle CAD = \angle GFH$$ …. (1)
|$$\because$$ ∆ ABC ~ ∆ FEG (given)
$$\therefore$$ They are equiangular also
$$\therefore \angle CAB = \angle GFE$$
i.e., $$\angle CAD = \angle GFH$$
$$\angle ACD = \angle FGH$$ … (2)
|$$\because$$ ∆ ABC ~ ∆ FEG
$$\therefore \angle ACB = \angle FGE$$
$$\Rightarrow \frac{1}{2} \angle ACB = \frac{1}{2} \angle FGE$$
(Halves of equal angles are equal)
$$\Rightarrow \angle ACD = \angle FGH$$
In view of (1) and (2),
∆ ACD ~ ∆ FGH
|AA similarity Criterion
$$\therefore \frac{CD}{GH} = \frac{AC}{FG}$$
|$$\because$$ corresponding sides of two similar triangles are proportional
ii) ∆ DCB ~ ∆ HGE
Sol.In ∆ DCB and ∆ HGE
∆ DBC ~ ∆ HEG … (1)
|$$\because$$ ∆ ABC ~ ∆ FEG
$$\therefore \angle ABC = \angle FEG$$
i.e., $$\angle DBC = \angle HEG$$
$$\angle DCB = \angle HGE$$ ….. (3)
|$$\because$$ ∆ ABC ~ ∆ FEG
$$\therefore \angle ACB = \angle FGE$$
$$\Rightarrow \frac{1}{2} \angle ACB = \frac{1}{2} \angle FGE$$
(Halves of equal angles are equal)
$$\Rightarrow \angle DCB = \angle HGE$$
In view of (1) and (2),
∆ DCB ~ ∆ HGE
|AA similarity criterion
(iii)∆ DCA ~ ∆ HGF
Sol.In ∆ DCA and ∆ HGF
$$\angle DAC = \angle HFG$$ …..(1)
|$$\because$$ ∆ ABC ~ ∆ FEG
$$\therefore \angle CAB = \angle GFE$$
i.e., $$\angle CAD = \angle GFH$$
i.e., $$\angle DAC = \angle HFG$$
$$\angle DCA = \angle HGF$$ ….. (2)
|$$\because$$ ∆ ABC ~ ∆ FEG
$$\therefore \angle ACB = \angle FGE$$
$$\Rightarrow \frac{1}{2} \angle ACB = \frac{1}{2} \angle FGE$$
(Halves of equal angles are equal)
$$\Rightarrow \angle DCA = \angle HGF$$
In view of (1) and (2),
∆ DCA ~ ∆ HGF
|AA similarity criterion
11.In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ ABD ~ ∆ ECF.
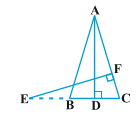
Sol.Given : E is a point on side CB produced of an isosceles triangle ABC with AB = AC.
Also, AD ⊥ BC and EF ⊥ AC.
To prove : ∆ ABD ~ ∆ ECF
Proof : In ∆ ABD and ∆ ECF,
$$\because$$ AB = AC
$$\therefore \angle ACB = \angle ABC$$
|Angles opposite to equal sides of triangle are equal
Interchanging LHS and RHS;
$$\Rightarrow \angle = \angle ACB$$
i.e., $$\angle ABD = \angle ECF$$
$$\angle ADB = \angle EFC$$
|Each equal to $$90^{0}$$
In view of (1) and (2),
∆ ABD ~ ∆ ECF
|AA similarity criterion
12.Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.
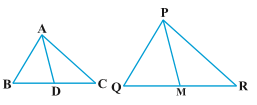
Sol.Given : Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR, i.e.,
$$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$$.
To Prove : ∆ ABC ~ ∆ PQR.
Proof : $$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$$
$$\Rightarrow \frac{AB}{PQ} = \frac{\frac{1}{2}BC}{\frac{1}{2}QR} = \frac{AD}{PM}$$
$$\Rightarrow \frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$$
[ $$\because$$ AD is median of $$\Delta ABC$$, therefore by definition of median, D is mid - point of BC. similarly M is mid-point of QR \right ]
i.e., ∆ ABD ~ ∆ PQM
|SSS similarity criterion
$$\therefore \angle ABD = \angle PQM$$
|$$\because$$ corresponding angles of two similar triangles are equal
i.e., $$\angle ABC = \angle PQR$$
Now, in ∆ ABC and ∆ PQR
$$\frac{AB}{PQ} = \frac{BC}{QR}$$ …. (1)
|Given
$$\angle ABC = \angle PQR$$
|proved above
In view of (1) and (2),
∆ ABC ~ ∆ PQR.
|SAS similarity criterion
13.D is a point on the side BC of a triangle ABC such that ∠ ADC = ∠ BAC. Show that $$CA^{2}$$ = CB.CD.
Sol.Given : D is a point on the side BC of a triangle ABC such that $$\angle ADC = \angle BAC$$.
To prove : $$CA^{2}$$ = CB. CD.
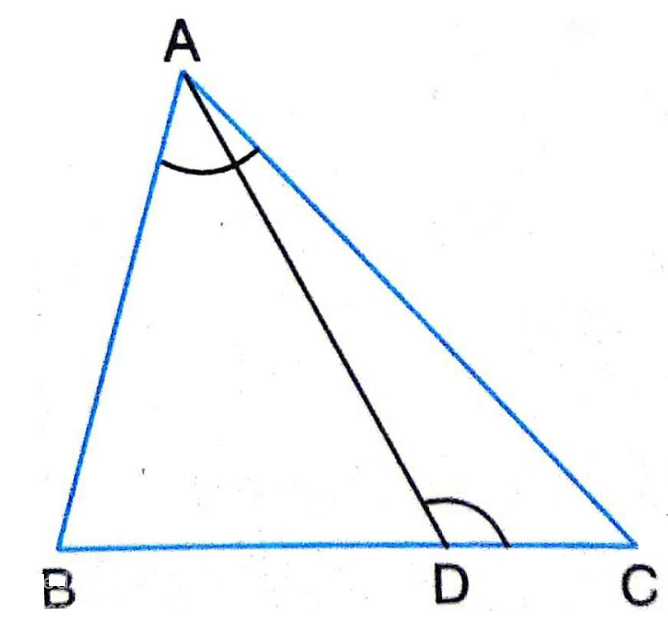
Proof : In $$\Delta BAC$$ and $$\Delta ADC$$,
$$\angle BAC = \angle ADC$$ |Given
$$\angle BCA = \angle DCA$$ |Common angle
$$\therefore \Delta BAC ~ \Delta ADC$$
|AA similarity criterion
$$\therefore \frac{CA}{CD} = \frac{CB}{CA}$$
|$$\because$$ corresponding sides of two similar triangles are proportional
Cross – multiplying
$$CA^{2}$$ = CB . CD.
14.Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ ABC ~ ∆ PQR.
Sol.See solution of Example 12.
15.A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Sol.
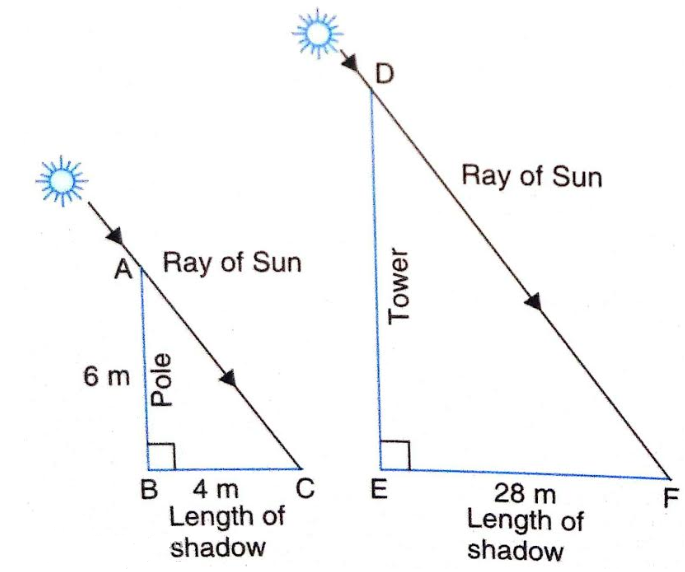
Let AB denote the vertical pole of length 6 m. BC is the shadow of the pole on the ground and BC = 4 m (given).
Let DE denote the tower. EF is the shadow of the tower on the ground.
EF = 28 m (given).
Let the height of the tower be h m.
In $$\Delta ABC$$ and $$\Delta DEF$$
$$\angle B = \angle E$$
|Each equal to $$90^{0}$$ because pole and tower are standing vertical to the ground
$$\angle A = \angle D$$
$$\therefore \Delta ABC ~ \Delta DEF$$
|AA similarity criterion
$$therefore \frac{AB}{DE} = \frac{BC}{EF}$$
|$$because$$ corresponding sides of two similar triangles are proportional
$$\Rightarrow \frac{6}{h} = \frac{4}{28} \Rightarrow$$ 4h = 6 X 28
$$\Rightarrow h = \frac{6 X 28}{4}$$ = 6 X 7
$$\Rightarrow $$ h = 42
Hence, the height of the tower is 42 m.
16.If AD and PM are medians of triangles ABC and PQR, respectively where ∆ ABC ~ ∆ PQR, prove that $$\frac{AB}{PQ} = \frac{AD}{PM}$$.
Sol.Given : AD and PM are medians of triangles ABC and PQR respectively where ∆ ABC ~ ∆ PQR
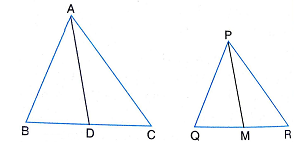
To prove : $$\frac{AB}{PQ} = \frac{AD}{PM}$$
Proof : ∆ ABC ~ ∆ PQR |Given
$$\therefore \frac{AB}{PQ} = \frac{BC}{QR}$$ …. (1)
|$$\because$$ Corresponding sides of two similar triangles are proportional
But BC = 2BD and QR = 2QM
($$\because$$ AD and PM are medians $$\Rightarrow$$ D and M are mid points of BC and QR respectively.)
Putting these values in (1),
$$\frac{AB}{PQ} = \frac{2BD}{2QM}$$
$$\Rightarrow \frac{AB}{PQ} = \frac{BD}{QM}$$ … (2)
Also, $$\angle B = \angle Q$$
|$$\because$$ ∆ ABC ~ ∆ PQR (given and hence their corresponding angles are equal
i.e., $$\angle ABD = \angle PQM$$ …. (3)
in view of (2) and (3),
∆ ABD ~ ∆ PQM
|SAS similarity criterion
$$\therefore \frac{AB}{PQ} = \frac{AD}{PM}$$
|$$\because$$ corresponding sides of two similar triangles are proportional
0 Doubts's