Exercise 6.4

1.Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.

Sol. ∆ ABC ~ ∆ DEF      |Given

$$\therefore \frac{ar(∆ ABC)}{ar(∆ DEF)} = (\frac{BC}{EF})^{2}$$

| $$\because$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

Putting given values,

$$\frac{64}{121} = (\frac{BC}{15.4})^{2} \Rightarrow (\frac{8}{11})^{2} = (\frac{BC}{15.4})^{2}$$

$$\Rightarrow \frac{8}{11} = \frac{BC}{15.4}$$        |Taking square root on both sides

Cross – multiplying

11 X BC = 8 X 15.4

$$\Rightarrow BC = \frac{8 X 15.4}{11}$$ = 8 X 1.4

$$\Rightarrow$$ BC = 11.2 cm.

2.Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Sol.In ∆ AOB and ∆ COD,

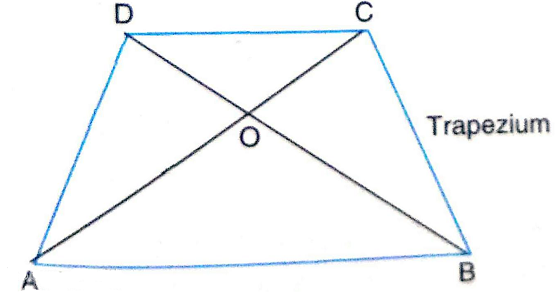
$$\angle AOB = \angle COD$$      |Vert.opp. $$\angle S$$

$$\angle OAB = \angle OCD$$     |Alt. Int. $$\angle S$$

[ $$\because$$ AB || DC (given)]

$$\therefore$$ ∆ AOB ~ ∆ COD

|AA similarity criterion

$$\therefore \frac{ar(∆ AOB}{ar(∆ COD)} = (\frac{AB}{CD})^{2}$$

| $$\because$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

= $$(\frac{2CD}{CD})^{2}$$        | $$\because$$ AB = 2CD (given)

= $$(\frac{2}{1})^{2} = \frac{4}{1}$$ = 4 : 1.

3.In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $$\frac{ar(ABC)}{ar(DBC)} = \frac{AO}{DO}$$ .

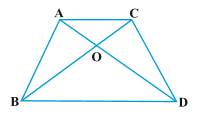
Sol.Given : In figure, ABC and DBC are two triangles on the same base BC and AD intersects BC at O.

To Prove : $$\frac{ar(∆ ABC)}{ar(∆ DBC)} = \frac{AO}{DO}$$

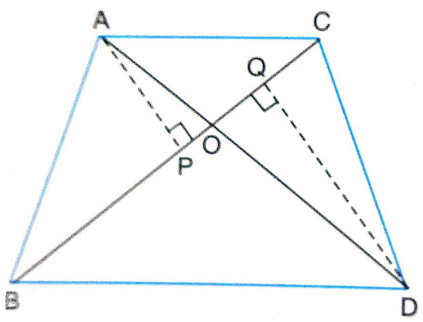
Construction : Draw $$AP \perp BC$$ and $$DQ \perp BC$$ .

Proof : In ∆ AOP and ∆ DOQ

$$\angle APO = \angle DQO$$

|Each equal to $$90^{0}$$ (By construction)

$$\angle AOP = \angle DOQ$$     |vert.opp. $$\angle S$$

$$\therefore$$ ∆ AOP ~ ∆ DOQ

|AA similarity criterion

$$\therefore \frac{AP}{DQ} = \frac{AO}{DO}$$       … (1)

| $$\because$$ Corresponding sides of two similar triangles are proportional

Now, $$\frac{ar(∆ ABC}{ar(∆ DBC} = \frac{\frac{1}{2}(BC)(AP)}{\frac{1}{2}(BC)(DQ)}$$

= $$\frac{AP}{DQ}$$

= $$\frac{AO}{DO}$$      |From ....     (1)

4.If the areas of two similar triangles are equal, prove that they are congruent.

Sol.Given : ∆ ABC and ∆ DEF are two similar triangle such that

ar(∆ ABC) = ar(∆ DEF)

To Prove : $$∆ ABC \cong ∆ DEF$$

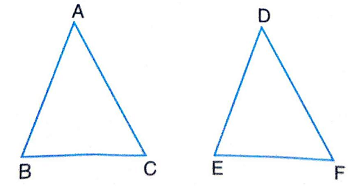
Proof : ∆ ABC ~ ∆ DEF      |Given

$$\therefore \frac{ar(∆ ABC)}{ar(∆ DEF)} = (\frac{BC}{EF})^{2}$$

| $$\therefore$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

But ar (∆ ABC) = ar (∆ DEF) (given)

$$\Rightarrow 1 = (\frac{BC}{EF})^{2}$$

Taking square roots,

1 = $$\frac{BC}{EF}$$

$$\Rightarrow$$ BC = EF      … (1)

Also, $$\angle B = \angle E$$       …. (2)

and $$\angle C = \angle F$$    … (3)

| $$\because$$ ∆ ABC ~ ∆ DEF   (given)

In view of (1), (2) and (3),

$$∆ ABC \cong ∆ DEF$$

|ASA congruence criterion

5.D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Sol.Given :D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ ABC.

To Determine. Ratio of the areas of ∆ DEF and ∆ ABC.

Determination.

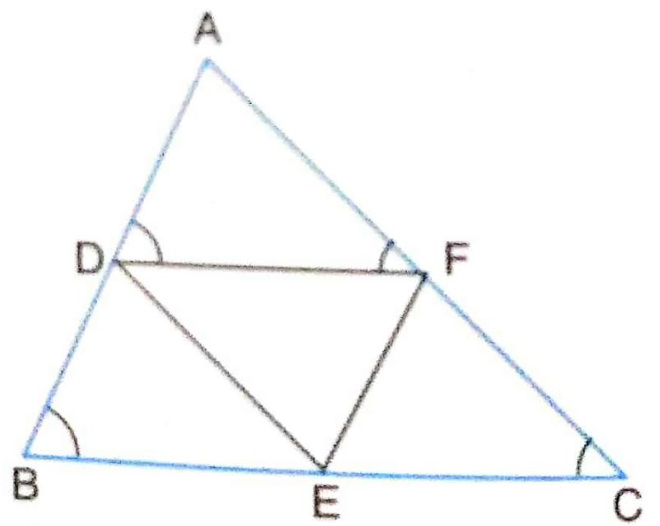
Because D and E are mid – points of sides AB and BC respectively  of ∆ ABC (given),

$$\therefore$$ DE || AC i.e., DE || AF

Similarly EF || AD

$$\therefore$$ Quadrilateral ADEF is a parallelogram

$$\angle DEF = \angle A$$

[ $$\because$$ Opposite angles of a parallelogram are equal]

Arguing as above, BEFD is also a parallelogram.

$$\therefore \angle DFE = \angle B$$     … (2)

[ $$\because$$ Opposite angles of a parallelogram are equal]

In view of (1) and (2),

∆ DEF ~ ∆ ABC

|AA similarity criterion

$$\therefore \frac{ar(∆ DEF)}{ar(∆ ABC)} = (\frac{DF}{BC})^{2}$$

| $$\because$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

= $$\left ( \frac{\frac{1}{2}BC}{BC} \right )^{2}$$

| $$\because$$ D and F are the mid-points of AB and AC respectively $$\therefore$$ DF || BC   and DF = $$\frac{1}{2} BC$$

= $$(\frac{1}{2})^{2} = \frac{1}{4}$$

$$\therefore$$ ar (∆ DEF): ar (∆ ABC) = 1 : 4.

Remark. $$\therefore$$ ar (∆ ABC) : 4 ar (∆ DEF)

6.Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Sol.Given : Two triangles ABC and DEF such that

∆ ABC ~ ∆ DEF

Let AM and DN be their corresponding medians.

To Prove : $$\frac{ar(∆ ABC)}{ar(∆ DEF)} = (\frac{AM}{DN})^{2}$$

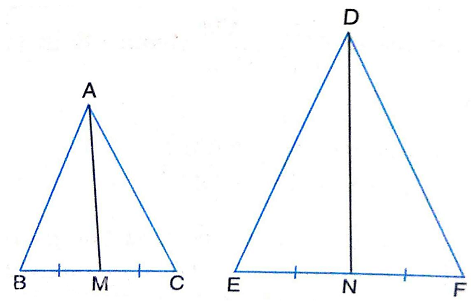
Proof : ∆ ABC ~ ∆ DEF        |Given

$$\therefore \frac{ar(∆ ABC)}{ar(∆ DEF)} = (\frac{AB}{DE})^{2}$$       ….. (1)

| $$\because$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides and $$\frac{AB}{DE} = \frac{BC}{EF}$$

| $$\because$$ The corresponding sides of two similar triangles are proportional

$$\Rightarrow \frac{AB}{DE} = \frac{2BM}{2EN}$$

| $$\because$$ AM and DN are the medians $$\Rightarrow$$ M is mid-point of BC and N is mid-point of EF.

= $$\frac{BM}{EN}$$    …. (2)

Also, $$\angle ABM = \angle DEN$$     …. (3)

| $$\because$$ ∆ ABC ~ ∆ DEF

$$\therefore \angle ABC = \angle DEF$$

(Corresponding angles of two similar triangles are equal)

In view of (2) and (3),

∆ ABM ~ ∆ DEN

|SAS similarity criterion

$$\therefore \frac{AB}{DE} = \frac{BM}{EN} = \frac{AM}{DN}$$     …. (4)

| $$\because$$ Corresponding sides of two similar triangles are proportional

Putting $$\frac{AB}{DE} = \frac{AM}{DN}$$ from (4) in (1), we have

$$\frac{ar(∆ ABC)}{ar(∆ DEF)} = (\frac{AM}{DN})^{2}$$ .

7.Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Sol.Given : ABCD is a square whose one diagonal is AC.

∆ BQC and ∆ APC are two equilateral triangles described on the side BC and diagonal AC of the square ABCD.

To Prove : ar (∆ BQC) = $$\frac{1}{2}$$ ar(∆ APC)

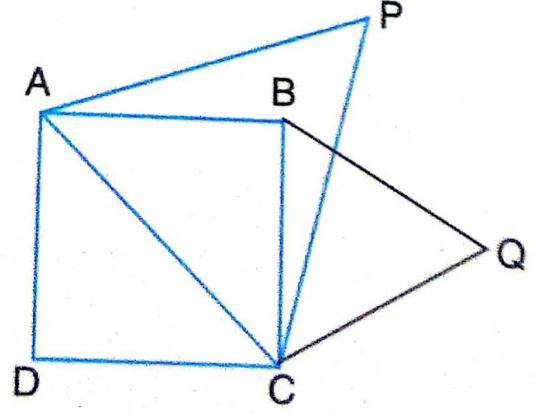
Proof : $$\because$$ ∆ APC and ∆ BQC are both equilateral triangles

$$\therefore$$ ∆ APC ~ ∆ BQC

|AAA similarity criterion

$$\therefore \frac{ar(∆ APC)}{ar(∆ BQC)} = (\frac{AC}{BC})^{2}$$

| $$\therefore$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

= $$(\frac{\sqrt{2}BC}{BC})^{2}$$

| $$\because$$ Diagonal of square = $$\sqrt{2}$$ side

= $$(\sqrt{2})^{2}$$ = 2

$$\Rightarrow \frac{ar(∆ APC)}{ar(∆ BQC)}$$ = 2

Cross – multiplying

2 ar (∆ BQC) = ar (∆ APC)

$$\Rightarrow ar (∆ BQC) = \frac{1}{2} ar(∆ APC)$$ .

TICK the correct answer and justify :

8.ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(A)2 : 1      (B)1 : 2         (C)4 : 1          (D)1 : 4.

Sol. $$\because$$ ∆ ABC and ∆ BDE are both equilateral triangles

$$\therefore$$ ∆ ABC ~ ∆ BDE

|AAA similarity criterion

$$\therefore \frac{ar(∆ ABC)}{ar(∆ BDE)} = (\frac{AB}{BD})^{2}$$

| $$\because$$ The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

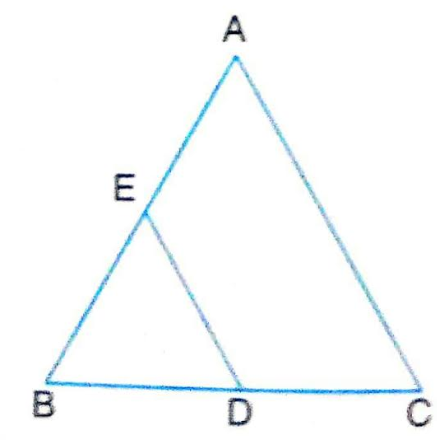
= $$(\frac{BC}{BD})^{2}$$         | $$\because$$ AB = BC = CA for equilateral ∆ ABC

= $$(\frac{2BD}{BD})^{2}$$

| $$\because$$ D is the mid – point of BC

= $$\frac{4}{1}$$

$$\Rightarrow$$ ar (∆ ABC) : ar (∆ BDE) = 4 : 1

Hence, (C) 4 : 1 is the correct answer.

9.Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio

(A)2 : 3         (B)4 : 9            (C)81 : 16           (D)16 : 81

Sol.Ratio of the areas of these triangles = $$4^{2} : 9^{2}$$

| $$\because$$ The ratio of the similar triangles is equal to the square of the ratio of their corresponding sides

Hence, (D) 16 : 81 is the correct answer.

Please Login For Further Details...

Submit