7.3 Section Formula

Suppose a telephone company wants to position a relay tower at P between A and B is such a way that the distance of the tower from B is twice its distance from A. If P lies on AB, it will divide AB in the ratio 1 : 2 (see Fig. 7.9).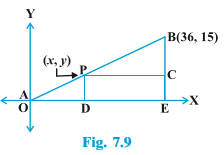If we take A as the origin O, and 1 km as one unit on both the axis, the coordinates of B will be (36, 15). In order to know the position of the tower, we must know the coordinates of P.

Let the coordinates of P be (x, y). Draw perpendiculars from P and B to the x-axis, meeting it in D and E, Draw PC perpendicular to BE. Then, by the AA similarity criterion,

Therefore , $$\frac{OD}{PC}=\frac{OP}{PB}=\frac{1}{2}, and \frac{PD}{BC}=\frac{OP}{PB}=\frac{1}{2}$$

So,  $$\frac{x}{36-x}=\frac{1}{2}$$  and $$\frac{y}{15-y}=\frac{1}{2}$$.

 These equations give x = 12 and y = 5.

You can check that P(12, 5) meets the condition that OP : PB = 1 : 2.

Consider any two points $$A(x _1, y_ 1)$$ and $$B(x_ 2, y_2)$$ and assume that P (x, y) divides AB internally in the ratio $$m_1 : m_2$$, i.e.,

$$\frac{PA}{PB}=\frac{m_1}{m_2}$$

Draw AR, PS and BT perpendicular to the x-axis. Draw AQ and PC parallel to the x-axis. Then, by the AA similarity criterion,

$$\Delta PAQ ~ \Delta BPC$$

Therefore, $$\frac{PA}{BP}=\frac{AQ}{PC}=\frac{PQ}{BC}$$...........(1)

Now,  $$AQ = RS = OS – OR = x – x1$$

$$PC  = ST = OT – OS = x_2 – x$$

$$PQ = PS – QS = PS – AR = y – y_1$$

$$BC = BT– CT = BT – PS = y_2 – y$$

Substituting these values in (1), we get

$$\frac{m_1}{m_2}=\frac{x-x_1}{x_2-x}=\frac{y-y_1}{y_2-y}$$

Taking

$$\frac{m_1}{m_2}=\frac{x-x_1}{x_2-x}, we \:\:get\:\: x=\frac{m_1x_2+m_2x_1}{m_1+m_2}$$

Similarly, taking   $$\frac{m-1}{m_2}=\frac{y-y_1}{y_2-y}$$, we get $$y=\frac{m_1y_2+m_2y_1}{m_1+m_2}$$

So, the coordinates of the point P(x, y) which divides the line segment joining the points $$A(x_1, y_1)$$ and $$B(x_2, y_2)$$ internally, in the ratio m_1 : m_2 are

$$(\frac{m_1x_2+m_2x_1}{m_1+m_2}, \frac{m_1y_2+m_2y_1}{m_1+m_2})$$…………..(2)

This is known as the section formula.

This can also be derived by drawing perpendiculars from A, P and B on the y-axis and proceeding as above.

If the ratio in which P divides AB is k : 1, then the coordinates of the point P will be

$$(\frac{kx_2+x_1}{k+1}, \frac{ky_2+y_1}{k+1})$$

Special Case : The mid-point of a line segment divides the line segment in the ratio 1 : 1. Therefore, the coordinates of the mid-point P of the join of the points $$A(x_ 1, y_1) and B(x _2, y_2)$$ is

$$(\frac{1.x_1+1.x_2}{1+1}, \frac{1.y_1+1.y_2}{1+1})=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$$

Example 6 : Find the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally.

Solution : Let P(x, y) be the required point. Using the section formula, we get

$$x=\frac{3(8)+1(4)}{3+1}=7, y=\frac{3(5)+1(-3)}{3+1}=3$$

Therefore, (7, 3) is the required point.

Example 7 : In what ratio does the point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8)?

Solution : Let (– 4, 6) divide AB internally in the ratio m1 : m 2. Using the section formula, we get

$$(-4, 6)=(\frac{3m_1-6m_2}{m_1+m_2}, \frac{-8m_1+10m_2}{m_1+m_2})$$

Recall that if (x, y) = (a, b) then x = a and y = b.

So,    $$-4=\frac{3m_1-6m_2}{m_1+m_2}  and 6=\frac{-8m_1+10m_2}{m_1+m_2}$$

$$-4=\frac{3m_1-6m_2}{m_1+m_2}$$   gives us

$$-4m_1-4m_2=3m_1-6m_2$$

i.e.,     7m 1 = 2m2

i.e.,      m1 : m2 = 2 : 7

You should verify that the ratio satisfies the y-coordinate also.

Now $$\frac{-8m_1+10m_2}{m_1+m_2}$$=$$\frac{-8\frac{m_1}{m_2}+10}{\frac{m_1}{m_2}+1}$$

$$(Dividing \:\:throughout\:\: by\:\: m_2)$$

=$$\frac{-8X\frac{2}{7}+10}{\frac{2}{7}+1}=6$$

Therefore, the point (– 4, 6) divides the line segment joining the points A(– 6, 10) and B(3, – 8) in the ratio 2 : 7.

Alternatively : The ratio m1 : m2 can also be written as $$\frac{m_1}{m_2}$$ : 1 or k : 1. Let (-4, 6)

divide AB internally in the ratio k : 1. Using the section formula, we get

(-4, 6)=$$(\frac{3k-6}{k+1}, \frac{-8k+10}{k+1})$$…………..(2)

So,   $$-4=\frac{3k-6}{k+1}$$

i.e., – 4k – 4 = 3k – 6

i.e., 7k = 2

i.e., k : 1 = 2 : 7

You can check for the y-coordinate also.

So, the point (– 4, 6) divides the line segment joining the points A(– 6, 10) and B(3, – 8) in the ratio 2 : 7.

Example 8 : Find the coordinates of the points of trisection (i.e., points dividing in three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4).

Solution : Let P and Q be the points of trisection of AB i.e., AP = PQ = QB (see Fig. 7.11).

Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordinates of P, by applying the section formula, are

$$(\frac{1(-7)+2(2)}{1+2},\frac{1(4)+2(-2)}{1+2})$$, i.e.,(-1, 0)

Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are

$$(\frac{2(-7)+1(2)}{2+1}, \frac{2(4)+1(2)}{2+1})$$, i.e., (-4, 2)

Therefore, the coordinates of the points of trisection of the line segment joining A and B are (–1, 0) and (– 4, 2).

Example 9 : Find the ratio in which the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4). Also find the point of intersection.

Solution : Let the ratio be k : 1. Then by the section formula, the coordinates of the

point which divides AB in the ratio k : 1 are $$(\frac{-k+5}{k+1}, \frac{-4k-6}{k+1})$$.

This point lies on the y-axis, and we know that on the y-axis the abscissa is 0.

Therefore,    $$\frac{-k+5}{k+1}=0$$

So,   k=-5

That is, the ratio is 5 : 1. Putting the value of k = 5, we get the point of intersection as

$$(0, \frac{-13}{3})$$

Example 10 : If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.

Solution : We know that diagonals of a parallelogram bisect each other.

So, the coordinates of the mid-point of AC = coordinates of the mid-point of BD

Ie., $$(\frac{6+9}{2}, \frac{1+4}{2})=(\frac{8+p}{2}, \frac{2+3}{2})$$

i.e.,$$(\frac{15}{2}, \frac{5}{2})=(\frac{8+p}{2}, \frac{5}{2})$$

$$\frac{15}{2}=\frac{8+p}{2}$$

P=7