8.2 Trigonometric Ratios

Let us take a right triangle ABC as shown in Fig. 8.4.

Here, ∠ CAB (or, in brief, angle A) is an acute angle. Note the position of the side BC with respect to angle A. It faces ∠ A. We call it the side opposite to angle A.

AC is the hypotenuse of the right triangle and the side AB is a part of ∠ A. So, we call it the side adjacent to angle A.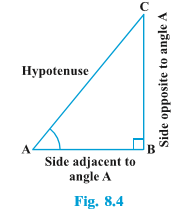the position of sides change when you consider angle C in place of A (see Fig. 8.5).

The trigonometric ratios of the angle A in right triangle ABC (see Fig. 8.4) are defined as follows :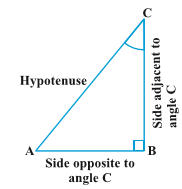Sine of $$\angle A=\frac{side\:L\: opposite\:\: to \:\:angle A}{hypotenuse}=\frac{BC}{AC}$$

Cosine of $$\angle A=\frac{side \:\:adjacent\:\: to \:\:angle A}{hypotenuse}=\frac{AB}{AC}$$

Tangent of $$\angle A=\frac{side\:\: opposite\:\: to \:\:angle A}{ side \:\:adjacent\:\: to\:\: angle A }=\frac{BC}{AB}$$

Cosecant of $$\angle A=\frac{1}{sine \:\:of\:\: \angle A}=\frac{hypotenuse}{side\:\: opposite\:\: to \:\:angle A}=\frac{AC}{BC}$$

Secant of $$\angle A=\frac{1}{cosine \:\:of \angle A}=\frac{hypotenuse}{side\:\: adjacent\:\: to \:\:angle A} =\frac{AC}{AB}$$

Cotangent of $$\angle A=\frac{1}{tangent \angle A}=\frac{side\:\: adjacent \:\:to\:\: angle A}{side opposite\:\: to \:\:angle A}=\frac{AB}{BC}$$

The ratios defined above are abbreviated as sin A, cos A, tan A, cosec A, sec A and cot A respectively. Note that the ratios cosec A, sec A and cot A are respectively, the reciprocals of the ratios sin A, cos A and tan A.

Also , observe that tan $$A=\frac{BC}{AB}=\frac{\frac{BC}{AC}}{\frac{AB}{AC}}=\frac{sin A}{cos A} and cot A =\frac{cos A}{sin A}$$

So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.

Example 1 : Given tan $$A =\frac{4}{3}$$, find the other trigonometric ration of the angle A.

Solution : Let us first draw a right ∆ ABC (see Fig 8.8).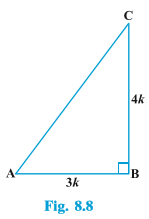Now , we know that tan $$A=\frac{BC}{AB}=\frac{4}{3}$$.

Therefore, if BC = 4k, then AB = 3k, where k is a positive number.

Now, by using the Pythagoras Theorem, we have

$$AC^{2} = AB^{2} + BC^{2} = (4k )^{2} + (3k)^{2} = 25k^{2}$$

So, AC = 5 k

Now, we can write all the trigonometric ratios using their definitions.

$$Sin A=\frac{BC}{AC}=\frac{4k}{5k}=\frac{4}{5}$$

$$Cos A=\frac{AB}{AC}=\frac{3k}{5k}=\frac{3}{5}$$

Therefore , $$cot A=\frac{1}{tan A}=\frac{3}{4},\:\: cosec A=\frac{1}{sin A}=\frac{5}{4}$$ and sec $$A=\frac{1}{cos A}=\frac{5}{3}$$.

Example 2 : If ∠ B and ∠ Q are acute angles such that sin B = sin Q, then prove that ∠ B = ∠ Q.

Solution : Let us consider two right triangles ABC and PQR where sin B = sin Q.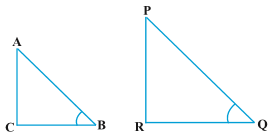We have     $$sin B=\frac{AC}{AB}$$

And    $$sin Q=\frac{PR}{PQ}$$

Then   $$\frac{AC}{AB}=\frac{PR}{PQ}$$

Therefore,   $$\frac{AC}{PR}=\frac{AB}{PQ}=k$$, say……………(1)

Now , using Pythagoras theorem,

$$BC=\sqrt{AB^{2}-AC^{2}}$$

And    $$QR=\sqrt{PQ^{2}-PR^{2}}$$

So, $$\frac{BC}{QR}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{PQ^{2}-PR^{2}}}=\frac{k^{2}PQ^{2}-k^{2}PR^{2}}{\sqrt{PQ^{2}-PR^{2}}}=\frac{k\sqrt{PQ^{2}-PR^{2}}}{\sqrt{PQ^{2}-PR^{2}}}=k$$…………(2)

From (1) and (2), we have

$$\frac{AC}{PR}=\frac{AB}{PQ}=\frac{BC}{QR}$$

Then, by using Theorem 6.4, ∆ ACB ~ ∆ PRQ and therefore, ∠ B = ∠ Q.

Example 3 : Consider ∆ ACB, right-angled at C, in which AB = 29 units, BC = 21 units and ∠ ABC = θ (see Fig. 8.10). Determine the values of

(i) $$cos^{2} θ + sin^{2} θ,$$

(ii) $$cos^{2} θ – sin^{2} θ$$.

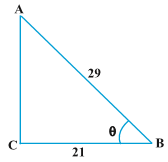
Solution : In ∆ ACB, we have

$$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{29^{2}-21^{2}}$$

=$$\sqrt{(29-21)(29+21)}=\sqrt{8X50}=\sqrt{400}=20$$ units

So, $$sin\theta = \frac{AC}{AB}=\frac{20}{29}, cos\theta =\frac{BC}{AB}=\frac{21}{29}.$$

i)$$cos^{2}\theta +sin^{2}\theta$$ =$$(\frac{20}{29})^{2}+(\frac{21}{29})^{2}=\frac{20^{2}+21^{2}}{29^{2}}=\frac{400+441}{841}=1$$

ii) $$cos^{2}\theta - sin^{2}\theta$$ =$$(\frac{20}{29})^{2}- (\frac{21}{29})^{2} =\frac{21+20)(21-20)}{29^{2}}=\frac{41}{841}$$

Example 4 : In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2  sin A cos A = 1.

Solution : In $$\Delta ABC,\:\: tan A=\frac{BC}{AB}=1$$

i.e.,           BC=AB

let AB=BC=k, where k is a positive number.

Now,    $$AC=\sqrt{AB^{2}+BC^{2}}$$

=$$\sqrt{k^{2}+k^{2}}=k\sqrt{2}$$

Therefore,  $$sin A=\frac{BC}{AC}=\frac{1}{\sqrt{2}}  and  cos A=\frac{AB}{AC}=\frac{1}{\sqrt{2}}$$

So,   $$2sin A cos A=2(\frac{1}{\sqrt{2}})(\frac{1}{\sqrt{2}})=1$$, which is the required value.

Example 5 : In ∆ OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig. 8.12). Determine the values of sin Q and cos Q.

Solution : In ∆ OPQ, we have

$$OQ^{2}=OP^{2}+PQ^{2}$$

i.e.,  $$(1+PQ)^{2}=OP^{2}+PQ^{2}$$

i.e.,   $$1+PQ^{2}+2PQ=OP^{2}+PQ^{2}$$

i.e., $$1+2PQ=7^{2}$$

i.e.,   PQ=24 cm  and OQ=1+PQ=25 cm

so,    $$ sin Q=\frac{7}{25} and Q=\frac{24}{25}.$$