3.1 INTRODUCTION

Let us  observe the two  situations

1. A flower bed in a garden is in the shape of a triangle. The longest side is 3 times the smallest side and the smallest side is 2 units shorter than the intermediate side. Let P represent the length of the smallest side. Then what is the perimeter in terms of P?

2. The length of a rectangular dining hall is twice its breadth. Let x represents the breadth of the hall. What is the area of the floor of the hall in terms of x?

In the above situations, there is an "unknown" in each. In the first situation, the smallest side is given as ‘P’ units

Since Perimeter of triangle = sum of all sides

Perimeter = P + 3P + P + 2

= 5P + 2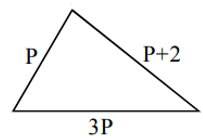

Similarly in the second situation, the length is given as twice the breadth.

So, if breadth = x, then length = 2x

Since the area of rectangle = lb

Area = (2x) (x)

= 2 $$x^{2}$$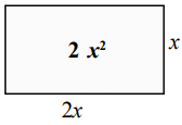

As you know, the perimeter, 5P + 2 of the triangle and the area 2$$x^{2}$$ of the rectangle are in the form of polynomials of different degrees.

3.2 WHAT ARE POLYNOMIALS?

A polynomial in x is an expression containing the sum of a finite number of terms of the form a$$x^{n}$$  for a real number a, where a $$\neq $$0 and a whole number n

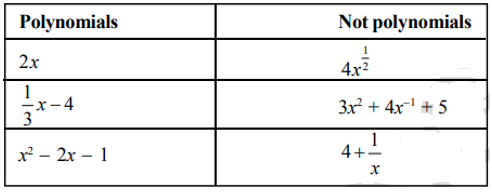3.2.1 DEGREE OF A POLYNOMIAL

Recall that if p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial p(x). For example, 3x + 5 is a polynomial in the variable x. It is of degree 1 and is called a linear polynomial. 5x, $$\sqrt{2y}+5,\frac{1}{3}p$$, m + 1 etc. are some more linear polynomials.

A polynomial of degree 2 is called a quadratic polynomial. For example, $$x^{2}$$ + 5x + 4 is