What We Have Discussed

1.Division Algorithm: Given positive integers a and b, there exist whole numbers q and r satisfying a = bq + r, 0 < r < b.

2.The Fundamental Theorem of Arithmetic states that every composite number can be expressed (factorized)

as a product of its primes, and this factorization is unique, apart from the order in which the prime factors occur.

3.If p is a prime and p divides a2, where a is a positive integer, then p divides a.

4.Let x be a rational number whose decimal expansion terminates. Then we can express x in the form of p/q , where p and q are coprime, and the prime factorization of q is of the form $$2^{n}5^{m}$$, where n and m are non-negative integers.

5.Let x = p/q be a rational number, such that the prime factorization of q is of the form $$2^{n}5^{m}$$, where n and m are non-negative integers. Then x has a decimal expansion which terminates.

6.Let x = p/q be a rational number, such that the prime factorization of q is not of the form $$2^{n}5^{m}$$, where n and m are non-negative integers. Then x has a decimal expansion which is non-terminating and repeating (recurring).

7.We define $$log_{a}$$ x = n, if $$a^{n} = x$$, where a and x are positive numbers and $$a \neq 1$$.

8.Laws of logarithms : If a, x and y are positive real numbers and $$a \neq 1$$, then

(i)$$log_{a} xy = log_{a} x + log_{a} y$$         (ii)$$log_{a} x/y = log_{a} x - log_{a} y$$
(iii)$$log_{a} x^{m} = m log_{a} x$$               (iv)$$log_{a}1 = 0$$
(v)$$log_{a} a = 1$$

9.Logarithms are used for calculations in engineering, science, business and economics.

 

1.1.INTRODUCTION

"God made the integers.  All else is the work of man" -  Leopold Kronecker

Life is full of numbers.  Imagine the moment you were born.  Your parents probably noted the time you were born, your weight, your length and the most important, counted your fingers and toes.  From then,  numbers accompany you throughout life.

Let us look in to a puzzle.

In a garden of flowers, a swarm of bees is setting in equal number on flowers. When they settle on two flowers, one bee will be left out. When they settle on three flowers, two bees will be left out. When they settle on four flowers, three bees will be left out. Similarly, when they settle on five flowers no bee will be left out. If there are at most fifty bees,

Let the number of bees be 'x'.  Then working backwards we see that x < 50.

Theorem-1.1 : (Division Algorithm) : Given positive integers a and b, there exist unique pair of integers q and r satisfying  a = bq + r,  0 < r < b.

This  result, was  first recorded  in  Book VII  of  Euclid's Elements.  Euclid's algorithm is based on this division algorithm.

Euclid's algorithm is a technique to compute the Highest common factor (HCF) of two given integers.  Recall that the HCF of two positive integers a and b is the greatest positive integer d that divides both a and b.

Let us find the HCF of 60 and 100, through the following activity.

Let us link the process  we follwed in the "Activity" to  Euclid's algorithm to get HCF of 60 and 100.

When 100 is divided by 60, the remainder is 40 100 = (60 X 1) + 40

Now consider the division of  60 with the remainder 40 in the above equation and apply the division algorithim

60 = (40 X 1) + 20

Now consider the division of  40 with the remainder 20, and apply the division lemma

40 = (20 X 2) + 0

Notice that the remainder has become zero and we cannot proceed any further.  We claim that the HCF of 60 and 100 is the divisor at this stage, i.e. 20.  (You can easily verify this by listing all the factors of 60 and 100.) We observe that it is a series of well defined steps to find HCF of 60 and 100.  So, let us state Euclid's algorithm clearly.

To obtain the HCF of two positive integers, say c and  d with c > d, follow the steps below:

Step1 :Apply Euclid's division lemma, to c and d. So, we find unique pair of whole numbers, q and r such that c = dq + r, 0 < r < d.

Step2 :If r = 0, d is the HCF of  c and d. If  r ¹ 0,  apply the division lemma to d and r.

Step3 :Continue the process till the remainder is zero.   The divisor at this stage will be the required HCF.

This algorithm works because HCF (c, d) = HCF (d, r) where the symbol HCF (m, n) denotes the HCF of any two positive integers m and n.

Example 1 : Show that  every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer

Solution : Let a be any positive integer and b = 2.  Then, by division algorithm, a = 2q + r, for some integer$$ q \geq  0$$, and  r = 0  or  r = 1, because $$0 \leq  r < 2.$$  So,  a = 2q  or  2q + 1.

If  a  is of the form 2q, then a is an even integer.  Also, a positive integer can be either even or odd.  Therefore, any positive odd integer is of the form 2q + 1.

1.2 THE FUNDAMENTAL THEOREM OF ARITHMATIC  

We know from Division Algorithm that for given positive integers a and b there exist unique pair of integers q and r satifying a = bq + r, 0 < r <b

From the above discussion you might have concluded that if   a  = bq,  'a' is divisible by 'b' then we can say that 'b' is a factor of 'a'.

For example we know that  24 =  2 x 12      

24 =  8 x 3

    =  2 x 2 x2 ·x3

We know that, if 24 = 2 x12 then we can say that 2 and 12 are factors of 24. We can also write 24 = 2 x 2 x2 x 3 and you know that this is the prime factorisation of 24.

Theorem-1.2 : (Fundamental Theorem of Arithmetic) : Every composite number can be expressed (factorised) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.

 the Fundamental Theorem of Arithmetic which says that every composite number can be factorized as a product of primes. Actually, it says more. It says that any given composite number can be factorized as a product of prime numbers in a ‘unique’ way, except for the order in which the primes occur. For example, when we factorize 210, we regard 2 x 3 x 5 x 7 as same as 3 x 5 x 7x 2, or any other possible order in which these primes are written. That is, given any composite number there is one and only one way to write it as a product of primes, as long as we are not particular about the order in which the primes occur.

In general, given a composite number x, we factorize it as $$x =p_1.p_2.p_3 .....p_n$$, where $$p_1, p_2, p_3...., p_n$$ are primes and written in ascending order, i.e., $$p1\leq p2\leq p3.....pn$$. If we combine the equal primes, we will get powers of primes. Once we have decided that the order will be ascending, then the way the number is factorised, is unique. For example, 27300 =  2 x2 x 3 x 5 x 5 x 7 x13 = 22x 3 x 52 x 7 x 13

Example 3.Consider the numbers of the form 4n where n is a natural number. Check whether there is any value of n for which $$4^{n}$$ ends with zero?

Solution : If $$4^{n}$$ is to end with zero for a natural number n, it should be divisible by 2 and 5. This means that the prime factorisation of $$ 4^{n}$$ should contain the prime number 5 and 2.

But it is not possible because $$4^{n} = (2)^{2n}$$  so 2 is the only prime in the factorisation of $$4^{n}$$. Since 5 is not present in the prime factorization, there is no natural number n for which 4n ends with the digit zero

Example 4: Find the  HCF and LCM  of 12 and 18 by the prime factorization method

Solution : We have 12 = 2 x 2 x 3 =  $$2^{2}$$ x  $$3^{1}$$

                             18 = 2 x 3 x 3 =  $$2^{1}$$ x  $$3^{2}$$

Note that HCF (12, 18) = $$2^{1}$$ x  $$3^{1}$$ = 6 = Product of the smallest power of each common prime factor of the numbers.

LCM (12, 18) = $$2^{2}$$ x  $$3^{2}$$ = 36 = Product of the greatest power of each prime factor of the numbers.

From the example above, you might have noticed that HCF (12, 18) · LCM [12, 18] = 12 · 18. In fact, we can verify that for any two positive integers a and b, HCF (a, b) ·  LCM [a, b] = a · b. We can use this result to find the LCM of two positive integers, if we have already found the HCF of the two positive integers.

1.2.1  Rational Numbers And Their Decimal Expansions

Till now we have discussed some properities of integers.  How can you find the preceeding or the succeeding integers for a given integer? You might have recalled that the difference between an integer and its preceeding or succeding integer is 1.  And by this property only you might have found required integers.

rational number,  say   $$\frac{p}{q}$$ ($$q \neq0$$)  and  explore  exactly  when  the  number   $$\frac{p}{q}$$  is a terminating

Let us consider the following terminating decimals.

 (i) 0.375     (ii) 1.04     (iii) 0.0875     (iv) 12.5

Now let us express them in $$\frac{p}{q}$$ form.

i)$$0.375=\frac{375}{1000}=\frac{375}{10^{3}}$$  

ii)$$1.04=\frac{104}{100}=\frac{104}{10^{2}}$$

iii)$$0.0875=\frac{875}{10000}=\frac{875}{10^{4}}$$  

iv)$$12.5=\frac{125}{10}=\frac{125}{10^{1}}$$

* We see that all terminating decimals taken by us can be expressed in $$\frac{p}{q}$$ form whose

denominators are powers of 10. Let us now factorize the numerator and denominator and then express then in the simplest form :

now

i)$$0.375=\frac{375}{10^{3}}=\frac{3X5^{3}}{2^{3}X5^{3}}=\frac{3}{2^{3}}=\frac{3}{8}$$

ii)$$1.04=\frac{104}{10^{2}}=\frac{2^{3}X13}{2^{2}X5^{4}}=\frac{26}{5^{2}}=\frac{26}{25}$$

iii)$$0.0875=\frac{875}{10^{4}}=\frac{5^{3}X7}{2^{4}X5^{4}}=\frac{7}{2^{4}X5}=\frac{7}{80}$$

iv)$$12.5=\frac{125}{10}=\frac{5^{3}}{2X5}=\frac{25}{2}$$

1.2.2 Non-Terminating, Recurring Decimals In Rational Numbers

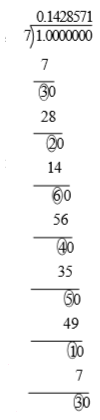Let us now consider rational numbers whose decimal expansions are non-terminating and recurring.

Let us look at the decimal conversion of  $$\frac{1}{7}$$

$$\frac{1}{7}$$  = 0.1428571428571 .....  which is a non-terminating and recurring decimal. Notice, the block of digits '142857' is repeating in the quotient.

Notice that the denominator  i.e., 7 can't be written in the form  $$2^{n}5^{m}$$

Example-5.  Using the above theorems, without actual division, state whether decimal form of the following rational numbers are terminating or non-terminating, repeating decimals

i)$$\frac{16}{125}$$      ii)$$\frac{25}{32}$$     

iii)$$\frac{100}{81}$$    iv)$$ \frac{41}{75}$$

solution : i)$$\frac{16}{125}=\frac{16}{5X5X5}=\frac{16}{5^{3}}$$

ii)$$\frac{25}{32}=\frac{25}{2X2X2X2X2}=\frac{25}{2^{2}}$$

iii)$$\frac{100}{81}=\frac{100}{3X3X3X3}=\frac{10}{3^{4}}$$has a non-terminating repeating decimal form

iv)$$\frac{41}{75}=\frac{41}{3X5X5}=\frac{41}{3X5^{2}}$$

1.3 IRRATIONAL NUMBERS

you were introduced to irrational numbers and some of their properties. You studied about their existence and how the rationals and the irrationals together made up the real numbers.  You even studied how to locate irrationals on the number line. However, we did not prove that they were irrationals.  In this section, we will prove that  $$\sqrt{2}$$, $$\sqrt{3}$$, $$\sqrt{5}$$in general is irrational, where p is a prime.  One of the theorems, we use in our proof, is the fundamental theorem of Arithmetic.

Recall, a real number  is called irrational if it cannot be written in the form

$$\frac{p}{q}$$, where p and q are integers and q¹0. Some examples of irrational numbers, with which you are already familiar, are : $$\sqrt{2}$$, $$\sqrt{3}$$, $$\sqrt{15}$$, , $$\pi$$ 0.10110111011110…, etc.

Before we prove that $$\sqrt{2}$$, is irrational, we will look at a theorem, the proof of which is based on the Fundamental Theorem of Arithimetic.

Theorem-1.6 : Let p be a prime number. If p divides $$a^{2}$$, (where a is a positive integer), then p divides a.

Proof : Let the prime factorization of  a  be  as follows :

$$a = p_1  p_2 … p_n, where p_1, p_2, …., p_n$$ are primes, not necessarily distinct.

Therefore $$a^{2} = (p_1p_2 … p_n) (p_1p_2 … p_n) = p^{2}_1p^{2}_2 … p^{2}_n$$

we are given that p divides $$a^{2}$$. Therefore, from the Fundamental Theorem of Arithmetic, it follows that p is one of the prime factors of $$a^{2}$$. the only prime factors of $$a^{2}$$ are

$$p_1 , p_2 ,… p_n. So,    p,    is    one,   of p_1, p_2, … p_n$$.

Now, since $$a = p_1p_2 … p_n,$$         p divides a.

Example 7.  Show that  $$\sqrt{2}$$ is irrational

If it is rational, then there must exist two integers r and s (s¹0) such that $$\sqrt{2}=\frac{r}{s}$$

If r and s have a common factor other than 1, then, we divide r and s by their highest

common factor to get $$\sqrt{2} =\frac{a}{b}$$, where a and b are co-prime. So, $$b\sqrt{2}=a$$

On squaring both sides and rearranging, we get $$2b^{2} = a^{2}$$. Therefore, 2 divides $$a^{2}$$

since 2 is dividing $$a^{2}$$, it also divides a.

So, we can write a = 2c for some integer c.

Substituting for a, we get $$2b^{2} = 4c^{2}$$, that is,$$ b^{2} = 2c^{2}$$.

This means that 2 divides $$b^{2}$$, and so 2 divides b ( using Theorem 1.6 with p= 2).

Therefore, both a and b have 2 as a common factor. But this contradicts the fact that a and b are co-prime

This contradiction has arisen because of our assumption that $$\sqrt{2}$$ is rational. Thus our assumption is false.  So, we conclude that $$\sqrt{2}$$ is irrational.

Example-8.  Show that $$5 – \sqrt{3}$$ is irrational.

Solution:Let us assume that $$5 – \sqrt{3}$$ is rational

That is, we can find coprimes a and b ($$b \neq0$$) such that $$5 –\sqrt{3}=\frac{a}{a}$$

Therefore, $$5-\frac{a}{a}=\sqrt{3}$$

We get $$\sqrt{3}=5-\frac{a}{a}$$

Since a and b are integers, $$5 – \sqrt{3}$$ is rational , and \sqrt{3} is also rational

But this contradicts the fact that $$\sqrt{3}$$ is irrational

This contradiction has arisen because of our assumption that $$5 – \sqrt{3}$$ is rational.

So, we conclude that $$5-\sqrt{5}$$ is irrational

Example-9.  Show that 3\sqrt{2} is irrational.

Solution : Let us assume, the contrary, that $$3\sqrt{2}$$ is rational

i.e., we can find co-primes a and b $$(b\neq0) such that 3\sqrt{2}=\frac{a}{a}$$

But this contradicts the fact that  $$\sqrt{2}$$  is irrational.

So, we conclude that $$3\sqrt{2}$$ is irrational.

Example-10.  Prove that $$\sqrt{2}+\sqrt{3}$$ is irrational.

Solution: Let us suppose that$$\sqrt{2}+\sqrt{3}$$ is rational

Let $$\sqrt{2}+\sqrt{3}=\frac{a}{b}, where a,b are integers and b\neq0$$

Therefore, $$\sqrt{2}=\frac{a}{b}-\sqrt{3}.$$

Squarring on both sides, we get

$$2=\frac{a^{2}}{b^{2}}+3-2\frac{a}{b}\sqrt{3}$$

Rearranging

$$\frac{2a}{b}\sqrt{3}=\frac{a^{2}}{b^{2}}+3-2$$

=$$\frac{a^{2}}{b^{2}}+1$$

$$\sqrt{3}=\frac{a^{2}+b^{2}}{2ab}$$

Since a, b are integers,$$ \frac{a^{2}+b^{2}}{2ab}$$ is rational, and so $$\sqrt{3}$$ is rational

This contradicts the fact that $$\sqrt{3}$$ is irrational . Hence $$\sqrt{2}+\sqrt{3}$$ is irrational.

1.4 EXPONENTIALS REVISED

We know the power 'an' of a number 'a'  with natural exponent 'n' is the product of 'n' factors each of which is equal to 'a’

i.e  $$a^{n}$$ = a.a.a…..

$$2^{0},2^{1},2^{3}$$.............power of 2

$$3^{0},3^{1},3^{3}$$…………………power of 3

We also know that when 81 is written as 34, it is said to be in exponential form. The number '4' is the 'exponent' or 'index' and 3 is the 'base'. we read it as " 81 is the 4th power of base 3".

EXPONENTIAL AND LOGARITHIMS

Let us Observe the following

$$2^{x}$$, = 4 =$$2^{2}$$,      gives x = 2

$$3^{y}$$, = 81 = $$3^{4}$$,   gives y = 4

$$10^{z}, = 100000 = 10^{5}$$,        gives z = 5

GRAPH OF EXPONENTIAL $$2^{x}$$, 

Let us draw the graph of $$y = 2^{x}$$,  

For this we compute the value of 'y' by choosing some values for 'x'

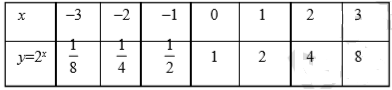
We plot the points and connect them with smooth curve

 

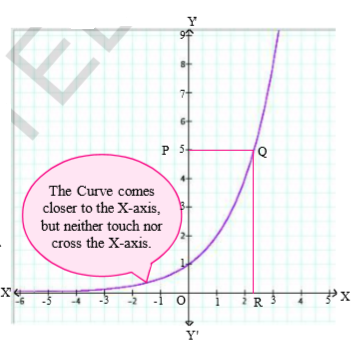
Note that as x increases, the value of  $$y = 2^{x}$$,   increases. As 'x' decreases the value of $$y = 2^{x}$$,   decreases very close to 0, but never attains the value 0.

Let us think, if  $$y = 2^{x}$$,  then for which value of x,  y becomes 5?

We know that in the graph Y-axis represents the value of  $$2^{x}$$, and X-axis represents the value of x. Locate the value of  5 on Y - axis, and represent it as a corresponding point "P" on Y-axis. Draw a line parallel to X-axis through P, which meets the graph at the point Q.

Now draw QR perpendicular to X-axis. Can we find the length of OR approximately from the graph? or where does it lie? Thus, we know that the x coordinate of the point R is the required value of  x, for which $$2^{x}=5.$$

This value of  x is called the logarithm of  5 to the base 2, written as $$log_{2}$$ 5.

PROPERTIES OF LOGARITHMS

Logarithms are more important in many applications, and also in advanced mathematics. We now establish some basic properties useful in manipulating expressions involving logarithms.

(i) The Product Rule

The properties of exponents correspond to properties of logarithms. For example, when we multiply with the same base, we add exponents.

$$a^{x}.a^{y}=a^{x+y}$$

This property of exponents coupled with an awareness that a logarithm is an exponent suggest the Product Rule.

(ii)The Quotient Rule

When we divide with the same base, we subtract exponents

$$\frac{a^{x}}{a^{y}}=a^{x-y}$$

This property suggests the quotient rule.

(iii) The Power Rule

When an exponential expression is raised to a power, we multiply the exponent

$$\left ( a^{m} \right )^{n}=a^{mn}$$       

This property suggests the power rule

Example-11.Expand $$log \frac{343}{125}$$

Solution : As you know, $$log_a\frac{x}{y}=log_ax-log_ay$$

So, $$log\frac{343}{125}=log343-log125$$

=$$log7^{7}-log5^{3}$$

=$$3log7-3log5$$            (since, $$log_aX^{2}$$=m $$log_ax$$)

So $$log\frac{343}{125}=3(log7-log5).$$

Example-12.write $$2log3+3log5-5log2$$ as a single logarithm.

Solution: $$2log3+3log5-5log2$$

=$$log3^{2}+log5^{3}-log2^{5}$$        (since in n $$log_a x=log_ax^{n}$$)

=$$log9+log125-log32$$

=$$log(9X125)-log32$$                 (since $$log_ax+log_ay=log_axy$$)

=$$log\frac{1125}{32}(since log_ax-log_ay=log_a\frac{x}{y})$$

Example-13.solve $$3^{x}=5^{x-2}$$

Solution : $$x log_{10}3=(x-2)log_{10}5$$

$$xlog_{10}3=xlog_{10}5-2log_{10}5$$

$$xlog_{10}5-2log_{10}5=xlog_{10}3$$

$$xlog_{10}5-xlog_{10}3=2log_{10}5$$

$$x=\frac{2log_{10}5}{log_{10}5-log_{10}3}$$

Example-14. Find x if $$2log5+\frac{1}{2}log9-log3=logx$$

Solution: log x =$$2log 5+\frac{1}{2}log 9-log3$$

=$$log5^{2}+log 9^{\frac{1}{2}}-log3$$

=$$log25+log\sqrt{9}-log3$$

=log25+log3-log3

log x =log 25

$$\therefore$$ x=25

Please Login For Further Details...

Submit