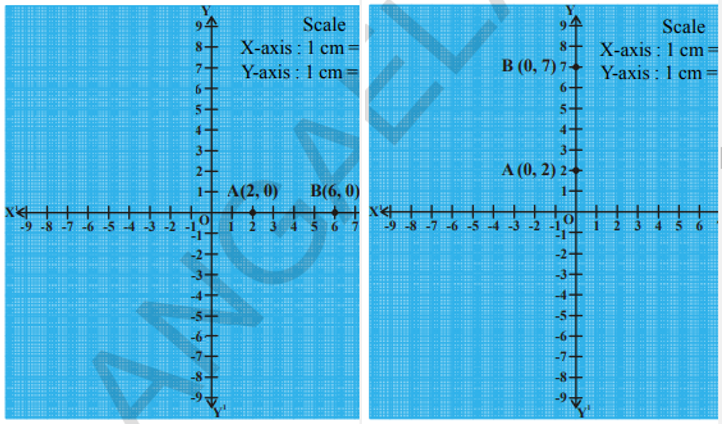
7.2 DISTANCE BETWEEN TWO POINTS

The two points (2, 0) and (6, 0) lie on the X-axis as shown in figure

It is easy to see that the distance between two points A and B as 4 units

We can say the distance between points lying on X-axis is the difference between the x-coordinates.

What is the distance between (-2, 0) and (-6, 0)?

The difference in the value of x-coordinates is

(-6) - (-2) = -4 (Negative) We never say the distance in negative values. So, we will take absolute value of the difference

Therefore, the distance = | (- 6) - (-2)| = |-4| = 4 units. So, in general for the points A(x 1 , 0), B(x 2 , 0) on the X-axis, the distance between A and B is |x 2 – x |

Similarly, if two points lie on Y-axis, then the distance between the points A and B would be the difference between their y coordinates of the points

The distance between two points (0, y 1 ) (0, y 2 ) would be |y 2 - y 1 |.

For example, let the points be A(0, 2) and B(0, 7)

Then, the distance between A and B is |7 - 2| = 5 units

7.3 DISTANCE BETWEEN TWO POINTS ON A LINE PARALLEL TO THE COORDINATE AXES.

Consider the points A(x 1 , y 1 ) and B(x 2 , y 1 ). Since the y-coordinates are equal, points lie on a line, parallel to X-axis.

AP and BQ are drawn perpendicular to X-axis.

Observe the figure. APQB is a rectangle.

Therefore, AB = PQ.

PQ = |x 2 - x 1 | (i.e., The modulus of difference between x coordinates)

Similarly, line joining two points A(x 1 , y 1 ) and B(x 1 , y 2 ) is parallel to Y-axis. Then the distance between these two points is |y 2 - y 1 | (It is read as modulus of the difference of y coordinates)

Example-1.  What is the distance between  A (4,0) and B (8, 0).

Solution : The abosolute value of the difference in the x coordinates is |x2 - x1| = |8 - 4| = 4 units

Example-2.   A and B are  two points  given by (8, 3), (-4, 3).  Find  the  distance  between A and B.

Solution : Here x1 and x2 are lying in two different quadrants and y-coordinate are equal. Distance AB = |x2 - x1| = |-4 - 8| = |-12| = 12 units

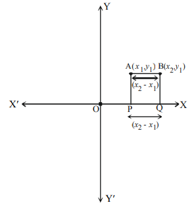
7.4 DISTANCE BETWEEN ANY TWO POINTS IN THE X-Y PLANE

Let A(x1 , y1 ) and B(x2 , y2 ) be any two points in a plane as shown in figure. Draw AP and BQ perpendiculars to X-axis Draw a perpendicular AR from the point A on BQ.

Then OP = x 1 , OQ = x2

So, PQ = OQ - OP = x2 - x1

Observe the shape of APQR. It is a rectangle.

So PQ = AR = x2 - x 1 .

Also QB = y2 , QR = y1 ,

So BR = QB - QR = y2 - y1

In DARB (right triangle)

$$AB^{2}=AR^{2}+RB^{2}$$ (By Pythagorean theorem)

$$AB^{2}=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$$

i.e.,AB = $$\sqrt{($$x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$

Hence, ‘d’ the distance between the points A and B is

d=$$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$

This is called the distance formula.Example-3. Let’s find the distance between two points A(4, 3) and B(8, 6)

Solution : Compare these points with (x 1 , y1 ), (x 2 , y 2 )

X1=4   x2=8     y1=3  y2=6

Using distance formula

d=$$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$

distance AB = =$$\sqrt{(x_{8}-x_{4})^{2}+(y_{6}-y_{3})^{2}}$$

$$\sqrt{4^{2}+3^{2}}$$

=$$\sqrt{16+9}=\sqrt{25}$$=5 units.

Example-4.  Show that the points A (4, 2), B (7, 5) and C (9, 7) are three points lying on a same line

Solution : Let us find the distances AB, BC, AC by using distance formula,

d=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

so, $$AB=\sqrt{(7-4)^{2}+(5-2)^{2}}=\sqrt{3^{2}+3^{2}}=\sqrt{9+9}=\sqrt{18}$$

=$$\sqrt{9x2}=3\sqrt{2}units$$.

BC=$$\sqrt{(9-7)^{2}+(7-5)^{2}}=\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}units$$

AC=$$\sqrt{(9-7)^{2}+(7-2)^{2}}=\sqrt{5^{2}+5^{2}}=\sqrt{25+25}=\sqrt{50}$$

=$$\sqrt{25x2}=5\sqrt{2}units$$.

Now  $$AB + BC =3\sqrt{2}+2\sqrt{2}=5\sqrt{2}=AC$$. Therefore, that the three points (4, 2), (7, 5) and

(9, 7) lie on a straight line.  (Points that lie on the same line are called collinear points).

Example-5.  Do the points (3, 2), (-2, -3) and (2, 3) form a triangle?

Solution : Let us apply the distance formula to find the lengths PQ, QR and PR, where P(3, 2),  Q(-2, -3) and R(2, 3) are the given points.  We have

$$PQ=\sqrt{(-2-3)^{2}+(-3-2)^{2}}=\sqrt{(-5)^{2}+(-5)^{2}}=\sqrt{25+25}=\sqrt{50}$$=7.07 units

$$QR= \sqrt{(-2-3)^{2}+(-3-2)^{2}}=\sqrt{(-5)^{2}+(-5)^{2}}=\sqrt{25+25}=\sqrt{50}$$=7.07 units

$$QR=\sqrt{(2-(-2))^{2}+(3-(-3))^{2}}=\sqrt{(4)^{2}+(6)^{2}}=\sqrt{52}$$=7.21 units

$$PR=\sqrt{(2-3)^{2}+(3-2)^{2}}=\sqrt{(-1)^{2}+1^{2}}=\sqrt{2}$$=1.41 units

Since the sum of any two of these lengths is greater than the third length, the points P, Q and R form a triangle and all the sides of triangle are unequal.

Example-6.  Show that the points (1, 7), (4, 2), (-1, -1) and (-4, 4) are the vertices of a square.

Solution : Let A(1, 7),  B(4, 2),  C(-1, -1)and D(-4, 4) be the given points.

One way of showing that ABCD is a square is to use the property that all its sides should be equal and both its diagonals should also be equal. Now, the sides are.

AB=$$\sqrt{(1-4)^{2}+(7-2)^{2}}=\sqrt{9+25}=\sqrt{34}$$

BC=$$\sqrt{(4+1)^{2}+(2+1)^{2}}=\sqrt{25+9}=\sqrt{34}$$units

CD=$$\sqrt{(-1+4)^{2}+(-1-4)^{2}}=\sqrt{9+25}=\sqrt{34}$$ units

DA=$$\sqrt{(-4-1)^{2}+(4-7)^{2}}=\sqrt{25+9}=\sqrt{34}$$ units

And diagonal are  AC=$$\sqrt{(1+1)^{2}+(7+1)^{2}}=\sqrt{4+64}=\sqrt{68}$$ units

BD=$$\sqrt{(4+4)^{2}+(2-4)^{2}}=\sqrt{64+4}=\sqrt{68}$$unit

Since  AB = BC = CD = DA  and AC = BD.  So all the four sides of the quadrilateral ABCD are equal and its diagonals AC and BD are also equal.  Therefore,  ABCD is square.

Example-7.  The figure shows the arrangement of desks in a class room. Madhuri, Meena, Pallavi are seated at A(3, 1), B(6, 4) and C(8, 6) respectively.

Do you think they are seated in a line ? Give reasons for your answer

Solution : Using the distance formula, we have.

$$AB=\sqrt{(6-3)^{2}+(4-1)^{2}}=\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$$

Units

BC=$$\sqrt{(8-6)^{2}+(6-4)^{2}}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$$units

AC=$$\sqrt{(8-3)^{2}+(6-1)^{2}}=\sqrt{25+25}=\sqrt{50}=5\sqrt{2}$$units

Since, $$AB + BC =3\sqrt{2}=2\sqrt{2}=5\sqrt{2}=AC$$ , we can say that the points A, B and C are collinear. Therefore, they are seated in a line.

Example-8.  Find the relation between x and y such that the point (x , y) is equidistant from the points (7, 1) and (3, 5).

Solution : Given  P(x, y) be equidistant from the points A(7, 1) and B(3, 5).

AP=BP.   So.$$AP^{2}=BP^{2}$$

i.e.,$$(x-7)^{2}+(y-1)^{2}=(x-3)^{2}+(y-5)^{2}$$

i.e.,$$(x^{2}-14x+49)+(y^{2}-2y+1)=(x^{2}-6x+9)+(y^{2}-10y+25)$$

$$(x^{2}+y^{2}-14x-2y+50)-(x^{2}+y^{2}-6x-10y+34)=0$$

-8x+8y=-16

i.e., x-y=2

Example-9.  Find a point on the Y-axis which is equidistant from both the points A(6, 5) and B(– 4, 3).

Solution : We know that a point on the Y-axis is of the form (0, y). So, let the point P(0, y) be equidistant from A and B. Then.

$$PA=\sqrt{(6-0)^{2}+(5-y)^{2}}$$

$$PB=\sqrt{(-4-0)^{2}+(3-y)^{2}}$$

$$PA^{2}=PB^{2}$$

So, $$(6-0)^{2}+(5-y)^{2}=(-4-0)^{2}+(3-y)^{2}$$

i.e., $$36+25+y^{2}-10y=16+9+y^{2}-6y$$

i.e., 4y=36

i.e.,y=9

So, the required point is (0, 9).

Let us check our solution :$$AP=\sqrt{(6-0)^{2}+(5-9)^{2}}=\sqrt{36+16}=\sqrt{52}$$

$$BP=\sqrt{(-4-0)^{2}+(3-9)^{2}}=\sqrt{16+36}=\sqrt{52}$$

So (0, 9) is equidistant from (6, 5) and (4, 3).

Exercise 7.1

1.Find the distance between the following pair of points.

(i)(2, 3) and (4, 1)

A.Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

=$$\sqrt{(4 - 2)^{2} + (1 - 3)^{2}}$$

=$$\sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$$ units.

(ii)(-5, 7) and (-1, 3)

A.Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

= $$\sqrt{(-1 + 5)^{2} + (3 - 7)^{2}}$$

= $$\sqrt{4^{2} + (-4)^{2}}$$

= $$\sqrt{16 + 16} = \sqrt{32}$$

= $$4\sqrt{2}$$ units.

(iii)(-2, -3) and (3, 2)

A.Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

= $$\sqrt{(3 + 2)^{2} + (2 + 3)^{2}}$$

= $$\sqrt{5^{2} + 5^{2}} = \sqrt{25 + 25}$$

= $$\sqrt{50} = 5\sqrt{2}$$ units.

(iv)(a, b) and (-a, -b)

A.Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

= $$\sqrt{(-a - a)^{2} + (-b - b)^{2}}$$

= $$\sqrt{4a^{2} + 4b^{2}}$$

= $$\sqrt{4(a^{2} + b^{2})} = 2\sqrt{a^{2} + b^{2}}$$

2.Find the distance between the points (0, 0) and (36, 15).

A.Given : Origin O(0, 0) and a point P (36, 15).

Distance between any point and origin = $$\sqrt{x^{2} + y^{2}}$$

$$\therefore$$ Distance = $$\sqrt{36^{2} + 15^{2}}$$

= $$\sqrt{1296 + 225}$$

= $$\sqrt{1521}$$ = 39 units.

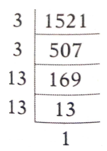
$$\therefore$$ 1521 = $$3^{2} X 13^{2}$$

$$\sqrt{1521}$$ = 3 X 13 = 39

3.Verify whether the points (1, 5), (2, 3) and (-2, -1) are collinear or not.

A.Given : A(1, 5), B(2, 3) and C(-2, -1)

Then distance  $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(2 - 1)^{2} + (3 - 5)^{2}}$$

= $$\sqrt{1 + 4}  = \sqrt{5}$$

BC = $$\sqrt{(-2 - 2)^{2} + (-1 - 3)^{2}}$$

= $$\sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$$

AC = $$\sqrt{(-2 - 1)^{2} + (-1 - 5)^{2}}$$

= $$\sqrt{9 + 36} = \sqrt{45}$$

Here the sum of no two segments is equal to third segment.

Hence the points are not collinear.

!! Slope of AB, $$m_{1} = \frac{3 - 5}{2 - 1} = - 2$$ Slope of BC, $$m_{2} = \frac{-1 - 3}{-2 - 2} = 1$$ $$m_{1} \neq m_{2}$$ Hence A, B, C are not collinear.

4.Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.

A.Let A = (5, - 2); B = (6, 4) and C = (7, -2).

Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(6 - 5)^{2} + (4 + 2)^{2}}$$

= $$\sqrt{1 + 36} = \sqrt{37}$$

BC = $$\sqrt{(7 - 6)^{2} + (-2 - 4)^{2}}$$

= $$\sqrt{1 + 36} = \sqrt{37}$$

AC = $$\sqrt{(7 - 5)^{2} + (-2 + 2)^{2}} = \sqrt{4}$$

Now we have, AB = BC.

$$\therefore \Delta$$ ABC is an isosceles triangle.

i.e., given points are the vertices of an isosceles triangle.

5.In a class room, 4 friends are seated at the points A, B, C and D as shown in Figure. Jarina and Phani walk into the class and after observing for a few minutes Jarina asks Phani “Don’t you notice that ABCD is a square?” Phani disagrees. Using distance formula, decide who is correct and why?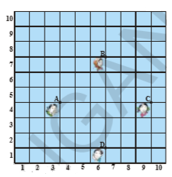A.Given : Four friends are seated at A, B, C and D where A (3, 4), B (6, 7), C (9, 4) and D(6, 1).

Now distance

$$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(6 - 3)^{2} + (7 - 4)^{2}}$$

= $$\sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$$

BC = $$\sqrt{(9 - 6)^{2}} + (4 - 7)^{2}$$

= $$\sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$$

CD = $$\sqrt{(6 - 9)^{2} + (1 - 4)^{2}}$$

= $$\sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$$

DA = $$\sqrt{(6 - 3)^{2} + (1 - 4)^{2}}$$

= $$\sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}$$

AC =$$ \sqrt{(9 - 3)^{2} + (4 - 4)^{2}} = \sqrt{36}$$ = 6

BD =$$ \sqrt{(6 - 6)^{2} + (1 - 7)^{2}} = \sqrt{36}$$ = 6

Hence in ABCD

four sides are equal

i.e., AB = BC = CD = DA = $$3\sqrt{2}$$ units

and two diagonals are equal.

i.e., AC = BD = 6 units.

$$\therefore$$ ABCD forms a square.

i.e., Jarina is correct.

6.Show that the following points form an equilateral triangle A(a, 0), B(-a, 0), C(0, $$\sqrt{3}$$).

A.Given : A (a, 0), B((-a, 0), C (0, $$\sqrt{3}$$)

Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(-a - a)^{2} + (0 - 0)^{2}}$$

= $$\sqrt{4a^{2}}$$ = 2a

BC = $$\sqrt{(0 + a)^{2} + (a\sqrt{3} - 0)^{2}}$$

= $$\sqrt{a^{2} + 3a^{2}} = \sqrt{4a^{2}}$$ = 2a

CA = $$\sqrt{(0 - a)^{2} + (a\sqrt{3} - 0)^{2}}$$

= $$\sqrt{a^{2} + 3a^{2}} = \sqrt{4a^{2}}$$ = 2a

Now, AB = BC = CA.

$$\therefore \Delta$$ is an equilateral triangle.

7.Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram.

A.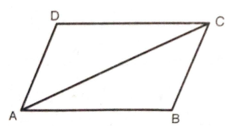Given : A (-7, - 3), B(5, 10), C(15, 8) and D(3, -5)

Distance = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(5 + 7)^{2} + (10 + 3)^{2}}$$

= $$\sqrt{144 + 169} = \sqrt{313}$$

BC = $$\sqrt{(15 - 5)^{2} + (8 - 10)^{2}}$$

= $$\sqrt{100 + 4} = \sqrt{104}$$

CD = $$\sqrt{(3 - 15)^{2} + (-5 - 8)^{2}}$$

= $$\sqrt{144 + 169} = \sqrt{313}$$

AD = $$\sqrt{(3 + 7)^{2} + (-5 + 3)^{2}}$$

= $$\sqrt{100 + 4} = \sqrt{104}$$

$$\therefore$$ In ABCD, both pairs of opposite sides (AB, CD) and (BC, AD) are equal.

Hence the given points form a parallelogram.

8.Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of a rhombus. Find its area.

(Hint : Area of rhombus = $$\frac{1}{2}$$ X product of its diagonals)

A.Given in ABCD, A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4)

Distance formula = $$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(-1 + 4)^{2} + (2 + 4)^{2}}$$

= $$\sqrt{9 + 81} = \sqrt{90}$$

=$$\sqrt{9 X 10} = 3\sqrt{10}$$

BC = $$\sqrt{(8 + 1)^{2} + (5 - 2)^{2}}$$

= $$\sqrt{81 + 9} = \sqrt{90} = 3\sqrt{10}$$

CD = $$\sqrt{(5 + 4)^{2} + (-4 - 5)^{2}}$$

= $$\sqrt{9 + 81} = \sqrt{90} = 3\sqrt{10}$$

AD = $$\sqrt{(5 + 4)^{2} + (-4 + 7)^{2}}$$

= $$\sqrt{81 + 9} = \sqrt{90} = 3\sqrt{10}$$

AC = $$\sqrt{(8 + 4)^{2} + (5 + 7)^{2}}$$

= $$\sqrt{144 + 144} = \sqrt{288} = 12\sqrt{2}$$

BD = $$\sqrt{(5 + 1)^{2} + (-4 - 2)^{2}}$$

= $$\sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2}$$

$$\therefore$$ In ABCD, AB = BC = CD = AD [from sides are equal]

Hence ABCD is a rhombus.

Area of a rhombus = $$\frac{1}{2} d_{1}d_{2}$$

= $$\frac{1}{2}$$ X $$12\sqrt{2} X 6\sqrt{2}$$

= 72 sq. units.

9.Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.

(i)( 1, -2), (1, 0), (-1, 2), (-3, 0)

A.Let A (- 1, -2), B(11, 0), C(- 1, 2), D(-3, 0) be the given points.

Distance formula

=$$\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$$

AB = $$\sqrt{(1 + 1)^{2} + (0 + 2)^{2}}$$

= $$\sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$$

BC = $$\sqrt{(-1 - 1)^{2} + (2 - 0)^{2}}$$

= $$\sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$$

CD = $$\sqrt{(-3 + 1)^{2} + (0 - 2)^{2}}$$

= $$\sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$$

AD = $$\sqrt{(-3 + 1)^{2} + (0 + 2)^{2}}$$

= $$\sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$$

AC = $$\sqrt{(- 1 + 1)^{2} + (2 + 2)^{2}}$$

= $$\sqrt{16}$$ = 4 units.

BD = $$\sqrt{(-3 - 1)^{2} + (0 - 0)^{2}}$$

= $$\sqrt{16}$$ = 4 units

In ABCD, AB = BC = CD = AD

- four sides are equal

AC = BD - diagonals are equal

Hence, the given points form a square.

(ii)(-3, 5), (3, 1), (1, -3), (-5, 1)

A.Let A(-3, 5), B(3, 1), C(1, -3) and D(-5, 1) be the given points

Distance formula

= $$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$

AB =$$\sqrt{(3+3)^{2}+(1-5)^{2}}$$

=$$\sqrt{36+16}=\sqrt{52}$$

=$$\sqrt{4x13}=2\sqrt{13}$$

BC = $$\sqrt{(3-2)^{2}+(1+3)^{2}}$$

$$\sqrt{(3-1)^{2}+(1+3)^{2}}$$

=$$\sqrt{4+16}=\sqrt{20}=2\sqrt{5}$$

CD = $$\sqrt{(1+5)^{2}+(-3-1)^{2}}$$

$$\sqrt{36+16}= \sqrt{52} = 2\sqrt{13}$$

DA= $$\sqrt{(-5+3)^{2}+(1-5)^{2}}$$

$$\sqrt{4+16}= \sqrt{20} = 2\sqrt{5}$$

$$\therefore $$ opposite sides are equal.

AC = $$\sqrt{(-3-1)^{2}+(5+3)^{2}}$$

$$\sqrt{16+64}= \sqrt{80} = 4\sqrt{5}$$

BD = $$\sqrt{(3+5)^{2}+(1-1)^{2}}$$

$$\sqrt{64+0}= \sqrt{64}$$ = 8

$$\therefore $$ its diagonal are not equa

In  ABCD, AB =CD, BC=AD and   AC $$\neq$$ BD

Hence ABCD is a parallelogram.

The given points form a parallelogram.

(iii)(4, 5), (7, 6), (4, 3), (1, 2)

Let  A (4,5), B (7,6) , C ( 4,3) and D (1,2) be the given points .

Distance formula

= $$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

AB = $$\sqrt{(7-4)^{2}+(6-5)^{2}}$$

$$\sqrt{9+1} = \sqrt{10}$$

BC =  $$\sqrt{(7-4)^{2}+(3-6)^{2}}$$

$$\sqrt{9+9} = \sqrt{18}$$=$$\sqrt{9 x 2}$$ = $$3\sqrt{2}$$

CD = $$\sqrt{(1-4)^{2}+(2-3)^{2}}$$

$$\sqrt{9+1} = \sqrt{10}$$

AD= $$\sqrt{(1-4)^{2}+(2-5)^{2}}$$

$$\sqrt{9+9} = \sqrt{18}$$= $$3\sqrt{2}$$

AC =  $$\sqrt{(4-4)^{2}+(3-5)^{2}}=\sqrt{4}$$=2

BD = $$\sqrt{(1-7)^{2}+(2-6)^{2}}$$

=$$\sqrt{36+16}=\sqrt{52}$$

In ABCD , AB = CD AND BC=AD (i.e both pairs of opposite sides are equal) and AC $$ \neq$$ BD

Hence ABCD is a parallelogram.

i.e., the given points form a parallelogram.

10.Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9).

Sol . given points , A(2,-5, B (-2,9).

Let P (X, 0) be the point on X- axis which is equidistant from A and B.

i.e ., PA =PB

distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

PA = $$\sqrt{(2-X)^{2}+(-5-0)^{2}}$$

=$$\sqrt{x^{2}-4x+4+25}$$

=$$\sqrt{x^{2}-4x+29}$$

PB = $$\sqrt{(-2-x)^{2}+(9-0)^{2}}$$

=$$\sqrt{x^{2}+4x+4+81}$$

=$$\sqrt{x^{2}+4x+85}$$

$$\Rightarrow \sqrt{x^{2}-4x+29}=\sqrt{x^{2}+4x+85}$$

squaring on both sides , we get

$$x^{2}-4x+29=x^{2}+4x+85$$

$$\Rightarrow -4x-4x=58-29$$

$$\Rightarrow -8x = 56$$

$$\Rightarrow x = \frac{56}{-8}=-7$$

$$\therefore$$ (x , 0)= (-7, 0) is the point which is equidistant from the given points.

11.If the distance between two points (x, 7) and (1, 15) is 10, find the value of x.
Sol. Given :A (x,7),B(1,15) and $$\overline{AB}$$ =10

Distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

$$\therefore \sqrt{(1-x)6{2}+(15-7)^{2}}$$=10

$$\Rightarrow \sqrt{1+x^{2}-2x+64}$$=10

$$\Rightarrow \sqrt{x^{2}-2x+65}$$=10

squaring both sides, we get

$$(\sqrt{x^{2}-2x+65})^{2}=10^{2}$$

$$\Rightarrow $X^{2}-2x+65$$=100

$$\Rightarrow X^{2}-7x+5x-35=0$$

$$\Rightarrow X(x-7)+5 (x-7)=0$$

$$\Rightarrow$$(x-7)(x+5)=0

$$\Rightarrow$$ x-7=0 or x+5=0

$$\Rightarrow$$ x=7   or x=-5

X = 7 or -5

12.Find the values of y for which the distance between the points P(2, -3) and

Q(10, y) is 10 units.

Sol . given : P (2, -3), Q (10, y) and  $$\overline{PQ}$$ =10

Distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

$$\Rightarrow \sqrt{(x_2-x_1)^{2}+(y+3)^{2}}$$

$$\Rightarrow \sqrt{(10-2)^{2}+(y+3)^{2}}=10$$

$$\Rightarrow \sqrt{64+y^{2}+6y+9}$$=10

$$\Rightarrow \sqrt{y^{2}+6y+73}$$=10

Squaring on both sides we get.

$$(\sqrt{y^{2}+6y+73})^{2}$$=10^{2}$$

$$Y^{2}$$+6y+73=100

$$Y^{2}$$+6y-27=0

$$Y^{2}$$+9y-3y-27=0

Y(y+9)-3(y+9)=0

(y+9)(y-3)=0

Y+9=0 or y-3=0

Y=-9 or y=3

Y=-9 or 3

13.Find the radius of the circle whose centre is (3, 2) and passes through (-5, 6).
Sol.

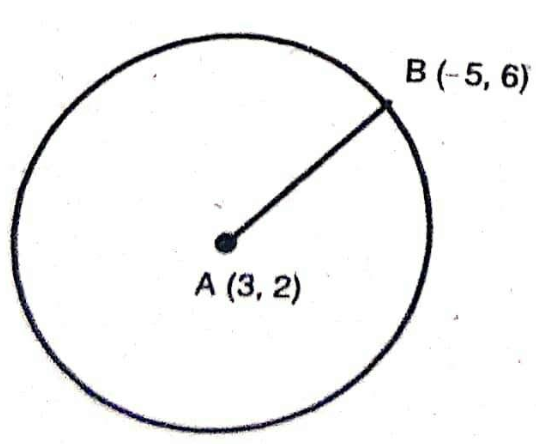
Given : A circle with centre A (3,2)

Passing through B(-5,6).

Radius =Ab

[ Distance of a point from the centre]

distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

Radius ‘r’ = $$\sqrt{(-5-3)^{2}+(6-2)^{2}}$$

=$$\sqrt{64+16}=\sqrt{80}$$

=$$\sqrt{16 x 5} = 4\sqrt{5}$$ units

14. Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14) ? Give reason
Let A (1 ,5) , B (5,8 ) and C (13, 14) be the given points

Distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

AB =  $$\sqrt{(5-1)^{2}+(8-5)^{2}}$$

=$$\sqrt{16+9} = \sqrt{25} $$=5

BC = $$\sqrt{(13-5)^{2}+(14-8)^{2}}$$

$$\sqrt{64+36} = \sqrt{100}$$=10

 

AC=$$ \sqrt{(13-1)^{2}+(14-5)^{2}}$$

$$\sqrt{144+81} = \sqrt{225}$$=15

Here, AC =AB+BC

$$\Delta$$ ABC cant be formed with the given vertices.

[$$\because $$ sum of the any two sides of triangles must be greater than the third side].

15.Find a relation between x  and  y  such that the point (x, y) is equidistant from the points (-2, 8) and (-3, -5)

Sol.A (-2,8) B (-3,-5) and P (x,y).

If P is equidistant from A, B, then PA=PB

Distance formula

=$$\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}}$$

=$$\sqrt{(x+2)^{2}+(y-8)^{2}}$$

=$$\sqrt{x^{2}+4x+4+y^{2}+64-16y}$$

=$$\sqrt{x^{2}+y^{2}+4x-16y+68}$$

Pb = $$\sqrt{(x+3)^{2}+(y+5)^{2}}$$

=$$\sqrt{x^{2}+6x+4+y^{2}+10y+25}$$

=$$\sqrt{x^{2}+y^{2}+6x+10y+34}$$

Now , PA =PB

$$\Rightarrow \sqrt{x^{2}+y^{2}+4x-16y+68}$$

=$$\sqrt{x^{2}+y^{2}+6x+10y+34}$$

Squaring on both sides we get,

$$X^{2}+y^{2}+4x-16y+68$$

$$X^{2}+y^{2}+6x+10y+34$$

$$\Rightarrow$$ 4x -16y -6x -10y=34-68

$$\Rightarrow$$-2x-26y = -34

$$\Rightarrow$$ x+13y=17 is the required condition.

Please Login For Further Details...

Submit