Exercise 4.4

 

1.In the given triangles, find out x,  y and  z

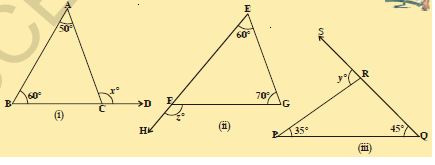
Sol. In fig(i)

$$x^{\circ}=50^{\circ}+60^{\circ}$$

( $$\therefore$$   exterior angle is equal to sum of the opposite interior angles)

$$\therefore$$ x= $$110^{\circ}$$

In fig (ii)

$$z^{\circ}=60^{\circ}+70^{\circ}$$

( $$\therefore$$   exterior angle is equal to sum of the opposite interior angles)

$$\therefore x=130^{\circ}$$

In fig(iii)

$$y^{\circ}=35^{\circ}+45^{\circ}$$ = $$80^{\circ}$$

( $$\therefore$$   exterior angle is equal to sum of the opposite interior angles)

2.In the given figure AS || BT; ∠4 = ∠5 $$\overline{SB}$$   bisects ∠AST. Find the measure of ∠1.

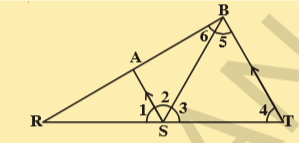
Sol. Given AS || BT

$$\angle 4=\angle 5$$ and $$\overline{SB}$$ bisects $$\angle AST$$ .

$$\therefore$$ BY PROBLEM

$$\angle 2=\angle 3$$ .........(i)

for the lines $$AS\parallel BT$$

$$\angle 2=\angle 5$$ ( $$\because$$ alternate interior angles)

$$\therefore$$ In $$\Delta BST$$

$$\angle 3=\angle 5=\angle 4$$

Hence $$\Delta BST$$ is equilateral triangle and each of its angle is equal to $$60^{\circ}$$

$$\therefore \angle 3=\angle 2=60^{\circ}$$

Now $$\angle 1+\angle 2+\angle 3=180^{\circ}$$

$$\therefore \angle 1+60^{\circ}+60^{\circ}=180^{\circ}$$

$$\because$$ angle at a point on a line

$$\therefore \angle$$ 1= $$180^{\circ}-120^{\circ}=60^{\circ}$$

3.In the given figure $$AB || CD; BC || DE$$ then find the values of x and y.

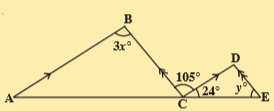
Sol.Given that $$AB || CD; BC || DE$$ .

$$\therefore$$ 3x= $$105^{\circ}$$ ( $$\because$$ alternate interior angles for $$AB\parallel CD$$ )

X= $$\frac{105^{\circ}}{3}$$ = $$35^{\circ}$$

Also $$BC\parallel DE$$

$$\therefore \angle D$$ = $$105^{\circ}$$

$$\because$$ alternate interior angles

Now in $$\Delta CDE$$

$$24^{\circ}+105^{\circ}+Y$$ = $$108^{\circ}$$

$$\because$$ angle sum property

$$\therefore y$$ = $$180^{\circ}-129^{\circ}$$ = $$51^{\circ}$$

4.In the adjacent figure $$BE ⊥ DA$$ and $$CD⊥DA$$ then prove that $$m∠1 ≅ m∠3$$ .

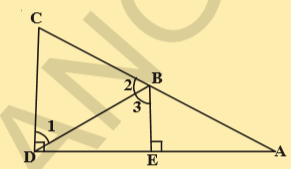
Sol.Given that $$CD⊥DA$$ and $$BE ⊥ DA$$ .

$$\Rightarrow$$ Two lines CD and BE are perpendicular to the same line DA.

$$\Rightarrow CD\parallel BE$$ (or)

$$\angle D=\angle E\Rightarrow CD\parallel BE$$

$$\because$$ corresponding angles for CD and BE and DA are transversal

Now $$m\angle 1=m\angle 3$$

$$\because$$ altenate interior angles for the lines $$CD\parallel BE ; DB$$ are transversal

Hence proved.

5.Find the values of x, y for which the lines AD and BC become parallel.

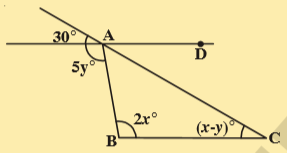
Sol.For the loines AD and BC to be parallel $$x-y- 30^{\circ}$$ (corresponding angles) ...........(1)

2x=8y ........(2)

( $$\because$$   alternate interior angles)

solving(1)&(2)

(1)x(2)=2x-2y=60

2         =2x-8y=0

                 6y=60

y= $$\frac{60}{6} =10^{\circ}$$

substituting y= $$10^{\circ}$$ in eq.(1)

$$x-10^{\circ}=30^{\circ}$$

$$\Rightarrow x=40^{\circ}$$

$$\therefore x=40^{\circ}$$ and $$y=10^{\circ}$$

6. Find the values of x and y in the figure.

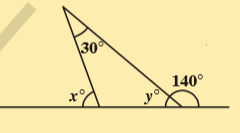
Sol.From the figure $$y+ 140^{\circ}=180^{\circ}$$

$$\because$$ linear pair of angles

$$\therefore y=180^{\circ}-140^{\circ}=40^{\circ}$$

and $$X^{\circ}=30^{\circ}+40^{\circ}=70^{\circ}$$

7.In the given figure segments shown by arrow heads are parallel. Find the values of x and y.

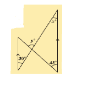Sol.From the figure

$$X^{\circ}=30^{\circ}$$ ( $$\because$$ alternate interior angles)

$$y^{\circ}=45^{\circ}+X^{\circ}$$ ( $$\because$$ exterior angles of a triangle =sum of opp.interior angles)

y= $$45^{\circ}+30^{\circ}=75^{\circ}$$

8. In the given figure sides QP and RQ of $$∠PQR$$ are produced to points S and T respectively. If  $$∠SPR = 135°$$ and  $$∠PQT = 110°$$ , find $$∠PRQ$$ .

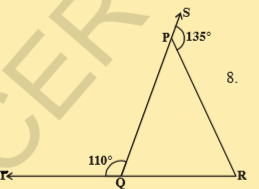
Sol.Given that $$\angle SPR =135^{\circ} and \angle PQT =110^{\circ}$$

From the figure

$$\angle SPR+\angle RPQ=180^{\circ}$$

$$\angle PQT+\angle PQR=180^{\circ}$$

[ $$\because$$ linear pair of angles ]

$$\Rightarrow \angle RPQ=180^{\circ}-\angle SPR$$

= $$180^{\circ}-135^{\circ}$$ = $$45^{\circ}$$

$$\Rightarrow \angle PQR=180^{\circ}-\angle PQT$$

= $$180^{\circ}-110^{\circ}=70^{\circ}$$

Now in $$\Delta PQR$$

$$\angle RPQ+\angle PQR+\angle PRQ=180^{\circ}$$

( $$\because$$ angle sum property)

$$\therefore 45^{\circ}+70^{\circ}+\angle PQR$$ = $$180^{\circ}$$

$$\therefore \angle PQR$$ = $$180^{\circ}-115^{\circ}$$ = $$65^{\circ}$$

9.In the given figure,  $$∠X = 62°,  ∠XYZ = 54°$$ . In $$ΔXYZ$$ If YO and ZO are the bisectors of  $$∠XYZ$$ and $$∠XZY$$ respectively find  $$∠OZY and  ∠YOZ$$ .

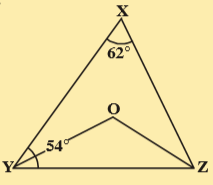
Sol.Given that $$∠X = 62°$$ ,  $$∠Y = 54°$$ . YO and ZO are the bisectors of  $$∠Y$$ and $$∠Z$$ in   $$\Delta XYZ$$

$$\angle X+\angle XYZ+\angle XZY$$ = $$180^{\circ}$$

$$62^{\circ}+54^{\circ}+\angle XZY$$ = $$180^{\circ}$$

$$\Rightarrow \angle XYZ$$ = $$180^{\circ}-116^{\circ}$$ = $$64^{\circ}$$

Also in $$\Delta OYZ$$

$$\angle OYZ$$ = $$\frac{1}{2}\angle XYZ$$ = $$\frac{1}{2}X54^{\circ}$$ = $$27^{\circ}$$

( $$\because$$ YO is bisector of $$\angle XYZ$$ )

$$\angle OZY$$ = $$\frac{1}{2}\angle XZY$$ = $$\frac{1}{2}X64^{\circ}$$ = $$32^{\circ}$$

( $$\because$$ OZ is bisector of $$\angle XYZ$$ )

And $$\angle OYZ+\angle OZY+\angle YOZ$$ = $$180^{\circ}$$

( $$\because$$ angle sum property, $$\Delta OYZ$$

$$\Rightarrow 27+32^{\circ}+\angle YOZ$$ = $$180^{\circ}$$

$$\Rightarrow \angle YOZ$$ = $$180^{\circ}-59^{\circ}$$ = $$121^{\circ}$$

10.In the given figure if $$AB || DE,  ∠BAC = 35° and ∠CDE = 53°, find  ∠DCE$$ .

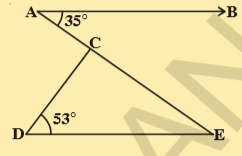
Sol.Given that $$AB || DE$$ , $$∠CDE = 53°$$ ; $$∠BAC = 35°$$

Now $$\angle E$$ = $$35^{\circ}$$

( $$\because$$ alternate interior angles)

Now in $$\Delta CDE$$

$$\angle C+\angle D+\angle E$$ = $$180^{\circ}$$

( $$\because$$ ANGLE SUM PROPERTY, $$\Delta CDE$$ )

$$\therefore \angle DCE+53^{\circ}+35^{\circ}$$ = $$180^{\circ}$$

$$\Rightarrow \angle DCE$$ = $$180^{\circ}-88^{\circ}$$ = $$92^{\circ}$$

11.In the given figure  if line segments PQ and RS intersect at point T, such that $$∠PRT = 40°,  ∠RPT = 95° and ∠TSQ = 75°, find  ∠SQT$$ .

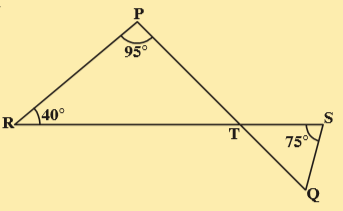
Sol.Given that $$∠PRT = 40°,  ∠RPT = 95° and ∠TSQ = 75°$$

In $$\Delta PRT\angle P+\angle R+\angle PTR$$ = $$180^{\circ}$$

( $$\because$$ angle sum property)

$$95^{\circ}+40^{\circ}+\angle PTR$$ = $$180^{\circ}$$

$$\Rightarrow \angle PTR$$ = $$180^{\circ}-135^{\circ}$$ = $$45^{\circ}$$

Now $$\angle PTR$$ = $$\angle STQ$$

( $$\because$$ vertically opposite angles)

In $$\Delta STQ\angle S+\angle Q+\angle STQ$$ = $$180^{\circ}$$

( $$\because$$ angle sum property)

$$75^{\circ}+\angle SQT+45^{\circ}$$ = $$180^{\circ}$$

$$\therefore \angle SQT$$ = $$180^{\circ}-120^{\circ}$$ = $$60^{\circ}$$

12.In the adjacent figure, ABC is a triangle in which $$∠B = 50° and ∠C = 70°$$ .  Sides AB and AC are produced. If ‘z’ is the measure of the angle between the bisectors of the exterior angles so formed, then find ‘z’

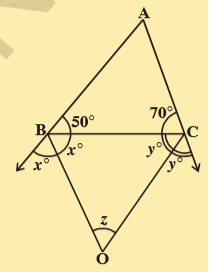
Sol.Given that $$\angle B$$ = $$50^{\circ}$$ ; $$\angle C=70^{\circ}$$

Angle between bisectors of exterior angles B and C is Z.

From the figure

$$50^{\circ}+2x$$ = $$180^{\circ}$$

70+2y= $$180^{\circ}$$

( $$\because$$ linear pair of angles)

$$\therefore$$ 2x= $$180^{\circ}-50$$

2x= $$130^{\circ}$$

x= $$\frac{130}{2}$$

= $$65^{\circ}$$

2y= $$180^{\circ}-70^{\circ}$$

2y= $$110^{\circ}$$

y= $$\frac{110^{\circ}}{2}$$

= $$55^{\circ}$$

Now in $$\Delta BOC$$

x+y+z= $$180^{\circ}$$ ( $$\because$$ angle sum property)

$$65^{\circ}+55^{\circ}+z$$ = $$180^{\circ}$$

z= $$180{\circ}-120^{\circ}$$ = $$60^{\circ}$$

 

Please Login For Further Details...

Submit