Introduction

Natural Numbers:

1. Non-negative counting numbers excluding zero are called Natural Numbers.

2. It is denoted as N = 1, 2, 3, 4, 5, ……….

Whole Numbers:

1. All-natural numbers including zero are called Whole Numbers.

2. It is denoted as W = 0, 1, 2, 3, 4, 5, …………….

Integers:

1. All-natural numbers, negative numbers and 0, together are called Integers.

2. It is denoted as Z = – 3, – 2, – 1, 0, 1, 2, 3, 4, …………..

Rational Numbers:

1. The number ‘a’ is called Rational if it can be written in the form of r/s where ‘r’ and ‘s’ are integers and s ≠ 0, Q = 2/3, 3/5, etc. all are rational numbers.

To find the rational number between two given numbers ‘a’ and ‘b’ is  (a+b)/2

Example:

Find 2 rational numbers between 4 and 5.

Sol: To find the rational number between 4 and 5  (a+b)/2 = (4+5)/2 = 9/2

To find another number we will follow the same process again.

(1/2) (4 + (9/2)) = (1/2) (17/2) = 17/4

Irrational Numbers:

The number ‘a’ which cannot be written in the form of p/q is called irrational, where p and q are integers and q ≠ 0 or you can say that the numbers which are not rational are called Irrational Numbers.

Example - √7, √11, etc.

Real Numbers:

1. All numbers including both rational and irrational numbers are called Real Numbers.

2. It is denoted as R = – 2, – (2/3), 0, 3 and √2

Real Numbers

All rational numbers can be written in the form of $$\frac{p}{q}$$, where p and q are integers and q ≠ 0. There are also other numbers that cannot be written in the form $$\frac{p}{q}$$, where p and q are integers and are called irrational numbers.

1. Rational Numbers:

If the rational number is in the form of a/b then by dividing a by b we can get two situations.

a. If the remainder becomes zero

While dividing if we get zero as the remainder after some steps then the decimal expansion of such number is called terminating.

Example: $$\frac{7}{8}$$ = 0.875

b. If the remainder does not become zero

While dividing if the decimal expansion continues and not becomes zero then it is called non-terminating or repeating expansion.

Example:  $$\frac{1}{3}$$ = 0.3333….

2.Irrational Numbers:

If we do the decimal expansion of an irrational number then it would be non–terminating non-recurring and vice-versa. i. e. the remainder does not become zero and also not repeated.

Example: π = 3.141592653589793238……

Representing Rational Numbers on Number line

Represent $$\frac{5}{3}$$ and  $$\frac{-5}{3}$$ on the number line.

Solution: Draw an integer line representing −2, −1, 0, 1, 2.

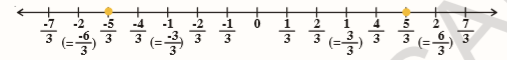
Representing Irrational Numbers on Number line

Example-1: Locate $$\sqrt{2}$$ on number line

Sol: At O draw a unit square OABC on a number line with each side 1 unit in length.

By Pythagoras theorem OB =$$\sqrt{1^2 +1^2}$$  = $$\sqrt{2}$$

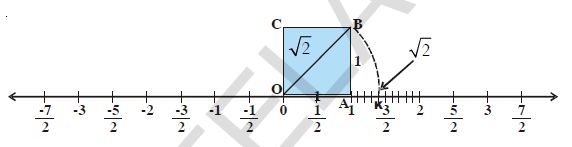
We have seen that OB = $$\sqrt{2}$$ Using a compass with center O and radius OB, draw an arc on the right side to O intersecting the number line at the point K. Now K corresponds to $$\sqrt{2}$$ on the number line.

Example-2: Locate $$\sqrt{3}$$ on the number line.

Sol: Let us return to the above fig.

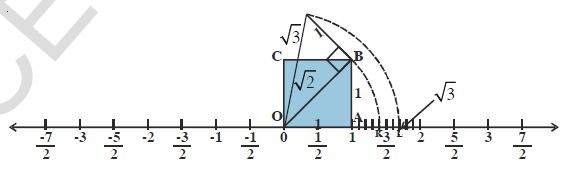
Now construct BD of 1 unit length perpendicular to OB as in Fig. Join OD

By Pythagoras theorem, OD = $$\sqrt{(\sqrt{2})^2 +1^2}$$ = $$\sqrt{2 + 1}$$ = $$\sqrt{3}$$

Using a compass, with center O and radius OD, draw an arc that intersects the number line at the point L right side to 0. Then ‘L’ corresponds to $$\sqrt{3}$$ . From this, we can conclude that many points on the number line can be represented by irrational numbers also. In the same way, we can locate n for any positive integers $$\sqrt{n}$$, after $$\sqrt{n - 1}$$ has been located.