Exercise 7.1

1.In quadrilateral ACBD, AC = AD and AB bisects   $$∠A$$ Show that  $$ΔABC≅  ΔABD$$. What can you say about BC and BD?

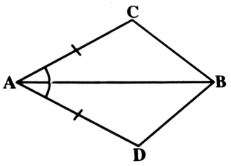
Sol.Given that AC=AD

$$ \angle BAC =\angle BAD $$  ($$\because$$ AB   bisects $$\angle a $$)

Now in $$ \Delta ABC$$ and $$\Delta ABD$$

AC=AD ($$\because$$ Given)

$$\angle$$ BAC= $$\angle BAD$$ ($$\because$$ given)

AB=AB (common side)

$$\therefore \Delta ABC\cong \Delta ABD$$

($$\because$$ SAS congruence rule)

2.ABCD is a quadrilateral in which AD = BC and $$ ∠DAB = ∠CBA $$ Prove that (i) $$ ΔABD≅  ΔBAC $$ (ii) BD = AC (iii) $$∠ABD = ∠BAC$$.

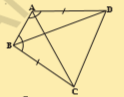
Sol.i)Given that AD=BC and $$\angle DAB=\angle CBA$$

Now in $$ \Delta ABD$$ and $$ \Delta BAC $$

AB=AB ($$\because$$ common side) 

AD=BC ($$\because$$ given)

$$\angle DAB=\angle CBA$$ ($$\because$$ given)

$$\therefore \Delta$$ ABD $$\cong \Delta BAC$$

($$\because$$  SAS congruence) 

ii)From i)AC=BD ($$\because$$ CPCT)

iii)$$\angle ABD=\angle$$ BAC [$$\because$$ CPCT from (1)]

3.AD and BC are equal and perpendiculars to a line segment AB.  Show that CD bisects AB.

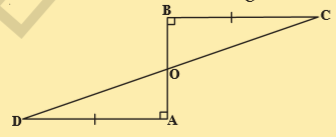
Sol.Given that $$AD=BS$$; $$AD\perp AB;BC\perp AB in \Delta BOC$$ and $$\Delta AOD$$

$$\angle BOC=\angle AOD$$ ($$\because$$ vertically opposite angles)

$$\angle OBC=\angle OAD$$ ($$\because$$ right angle)

BC=AD

($$\therefore  \Delta OBC\cong \Delta OAD$$) ($$\because AAS$$ )

$$\therefore$$ 'O'  bisects AB

Also OD=OC

$$\therefore$$ 'O' bisects CD

$$\Rightarrow$$ AB bisects CD

4.l and m are two parallel lines intersected by another pair of parallel lines p and q . Show that  $$ΔABC≅  ΔCDA$$

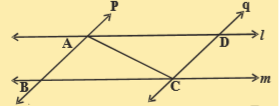
Sol.Given that l $$\parallel$$ m; p $$\parallel$$ q.

In $$ \Delta ABC and \Delta CDA $$

$$\angle BAC=\angle DCA$$ ($$\because$$ alternate interior angles)

$$\angle ACB=\angle CAD$$

AC=AC

$$\therefore \Delta ABC\cong \Delta CDA$$ ($$\because$$ ASA congruence)

5.In the adjacent figure,  AC = AE, AB = AD and $$\angle BAD = \angle EAC$$. Show that BC = DE.

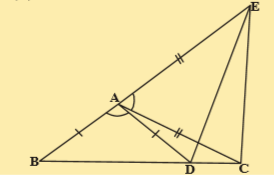
Sol.Given that AC=AE,AB=AD and $$\angle BAD=\angle EAC$$

$$In \Delta ABC$$ and $$\Delta ADE$$

AB=AE

AC=AE

$$\angle BAD=\angle EAC$$

$$\therefore \Delta ABC\cong \Delta ADE$$ ($$\because$$ SAS congruence)

$$\Rightarrow BC = DE(CPCT)$$

6.In right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB.  C is joined to M and produced to a point D such that DM = CM.  Point D is joined to point B (see figure).  Show that 

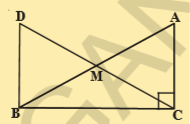i)$$ ΔAMC≅  ΔBMD $$

(ii)$$ ∠ DBC $$ is a right angle 

(iii)$$ΔDBC ≅  ΔACB$$

(iv)$$CM=\frac{1}{2}AB$$

Sol.Given that $$\angle c=90^{\circ}$$

M is mid point of AB;

DM=CM (i.e., M is mid point of DC)

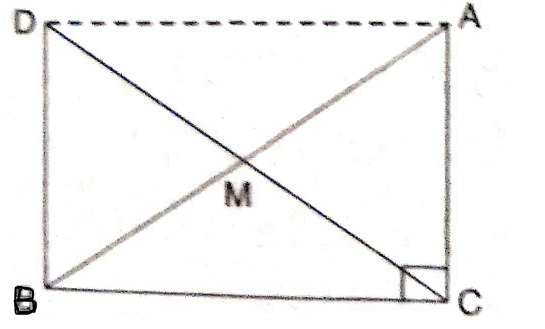i)In $$\Delta AMC$$ and $$\Delta BMD$$

AM=BM ($$\because$$ M is mid point of AB)

CM=DM ($$\because$$  M is mid point of CD)

$$\angle AMC=\angle BMD$$ ($$\because$$ vertically opposite angles)

$$\therefore \Delta AMC\cong \Delta BMD$$ ($$\because$$ SAS congruence)

ii)$$\angle MDB=\angle MCA$$ (CPCT of $$\Delta AMC$$ and $$\Delta BMD$$)

But these are alternate interior angles for the lines DB and AC and DC as transversal.

$$\therefore DB\parallel AC$$

As $$AC \perp BC ; DB$$ is also perpendicular to BC.

$$\therefore \angle DBC$$ is a right angle.

iii)in $$ \Delta DBC$$ and $$\Delta ACB$$

DB=AC (CPCT of $$\Delta BMD$$ and $$\Delta AMC$$)

$$\angle DBC=\angle ACB 90^{\circ}$$ (already proved)

BC=BC(common side)

$$\therefore \Delta DBC\cong \Delta ACB$$ (SAS congruence rule)

iv)DC=AB (CPCT of $$\Delta DBC$$ and $$\Delta ACB$$) $$\frac{1}{2}DC = \frac{1}{2}AB$$ (Dividing both sides by 2) 

CM= $$ \frac{1}{2} AB$$

7.In the adjacent figure ABCD is a square and$$ ΔAPB $$ is an equilateral triangle.  Prove that $$ ΔAPD≅  ΔBPC$$. [Hint : In $$ ΔAPD $$ and $$ ΔBPC  \overline{AD}= \overline{BC}$$, $$\overline{AP}$$=$$\overline{BP}$$ and $$∠PAD$$ = $$∠ PBC = 90^{\circ} - 60^{\circ}$$ = $$30^{\circ}]$$

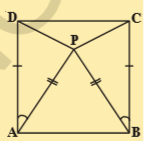Sol.Given that ABCD is a square.

$$\Delta APB$$ is an equilateral triangle.

Now in $$ \Delta APD$$ and $$\Delta BPC$$

AP=BP ($$\because$$ sides of an equilateral triangle)

AB=BC ($$\because$$ sides of a square)

$$\angle PAD=\angle PBC$$  [$$\because 90^{\circ}-60^{\circ}$$]

$$\therefore \Delta APD\cong \Delta BPC$$ (by SAS congruence)

8.In the adjacent figure   $$ΔABC$$ is isosceles as $$\overline{AB}=\overline{AC}$$ ;$$ \overline{BA}$$ and $$\overline{CA}$$ are produced to Q and P such that $$\overline{AQ} =\overline{AP}$$.Show that $$\overline{PB}=\overline{QC}$$.

(Hint:compare $$\Delta APB$$ and $$\Delta ACQ$$)

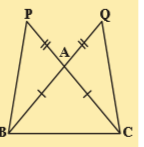
Sol.Given that $$\Delta ABC$$ is isosceles and AP=AQ

Now in $$\Delta APB$$ and $$\Delta AQC$$

AP=AQ (given)

AB=AC (given)

$$\angle PAB=\angle QAC$$ ($$\because$$ vertically opposite angles)

$$\therefore \Delta APB\cong \Delta AQC$$ (SAS congruence)

$$\therefore \overline{PB}=\overline{QC}$$ (CPCT of $$\Delta APB$$ and $$\Delta AQC$$)

9.In the figure given below $$\Delta ABC$$ , D is the midpoint of BC. $$DE\perp AB,DF\perp AC$$ and DE=DF. show that $$\Delta BED\cong \Delta CFD$$.

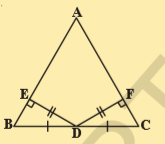
Sol.Given that D is the mid point of BC of $$\Delta ABC$$.

$$DF\perp$$ AC;DE=DF

$$DE\perp$$ AB

In $$\Delta BED$$ and $$\Delta CFD$$

$$\angle BED=\angle CFD$$ (given as $$90^{\circ}$$)

BD=CD ($$\because$$ D is mid point of BC)

ED=FD (given)

$$\therefore \Delta BED\cong \Delta$$ CFD(RHS congruence)

10.If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.

Sol.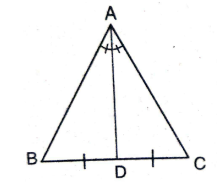Let $$\Delta ABC$$ be a triangle.

the bisector of $$\angle$$ A bisects BC

To prove: $$\Delta ABC$$ is isosceles (i.e.,AB=AC)

We know that bisector of vertical angle divides the base of the triangle in the ratio of other two sides.

$$\therefore \frac{AB}{AC}=\frac{BD}{BC}$$

Thus $$\frac{AB}{AC}$$ =1 ($$\because$$ given)

$$\Rightarrow$$ AB=AC

Hence the triangle is isosceles.

11.In the given figure ABC is a right triangle and right angled at B such that $$\angle ABC = 2 \angle BAC$$. Show that hypotenuse AC = 2BC.

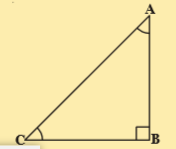
(Hint : Produce CB to a point D that BC = BD)

Sol.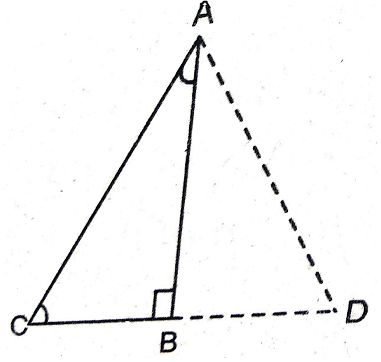Given that $$\angle B=90^{\circ};\angle BCA=2\angle BAC$$

To prove:AC=2BC

Produce CB to a point D such that

BC=BD

Now in $$\Delta ABC$$ and $$\Delta ABD$$

AB=AB (common)

BC=BD (construction)

$$\angle ABC=\angle ABD$$ ($$\because Each 90^{\circ}$$)

$$\therefore \Delta ABC\cong ABD$$

Thus AC=AD and $$\angle BAC=\angle BAD=30^{\circ}[CPCT]$$

$$[\because If \angle BAC=X then \angle BCA=2X $$

$$X+2x=90^{\circ}$$

$$3x=90^{\circ}$$

$$\Rightarrow X=30^{\circ}$$

$$\therefore \angle ACB=60^{\circ}]$$

Now in $$ \Delta ACD $$

$$\angle ACD=\angle ADC=\angle$$ CAD= $$60^{\circ}$$

$$\therefore \angle ACD$$ is equilateral $$\Rightarrow AC=CD=AD$$

$$\Rightarrow AC=2BC$$ ($$\because$$ C is mid point)

 

 

Please Login For Further Details...

Submit