what we are going to Learn..

1. If a linear equation has two variables then it is called a linear equation in two variables.
2.  Any pair of values of ‘x’ and ‘y’ which satisfy the linear equation in two variables is called its solution.
3. A linear equation in the two variables has many solutions.
4. The graph of every linear equation in two variables is a straight line.
5. An equation of the form y = mx represents a line passes through the origin.
6. The graph of x = k is a line parallel to Y-axis at a distance of k units and passes through the point (k, 0).
7. The graph of y = k is a line parallel to the X-axis at a distance of k units and passes through the point (0, k).
8. Equation of X-axis is y = 0.
9. Equation of Y-axis is x = 0.

Introduction

i) An equation of the form ax+bx+c=0 where a, b and c are real numbers such that a and b are not both zero is called a linear equation in two variables.

ii) A pair of values of x and y which satisfy the equation ax+bx+c=0 is called a solution of the equation.

iii) A linear equation in two variables has infinitely many solutions.

iv) The graph of every linear equation in two variables is a straight line.

v) y = 0 is the equation of x-axis and x = 0 is equation of y-axis.

vi) The graph of x=a is a straight line parallel to the y-axis.

vii) The graph of y = a is a straight line parallel to the x-axis.

viii) An equation of the type y = mx represents a line passing through the origin.

ix) Every point on the graph of a linear equation in two variables is a solution to the equation.

x) Conversely, every solution of the linear equation in two variables represents a point on the graph of the equation.

A solution of a Linear Equation

There is only one solution in the linear equation in one variable but there are infinitely many solutions in the linear equation in two variables. As there are two variables, the solution will be in the form of an ordered pair, i.e. (x, y). The pair which satisfies the equation is the solution of that particular equation.

Example:

1.Find the solution for the equation 2x + y = 7.

Solution:To calculate the solution of the given equation we will take x = 0

2(0) + y = 7

y = 7

Hence, one solution is (0, 7).

To find another solution we will take y = 0

2x + 0 = 7

x = 3.5

So another solution is (3.5, 0).

2.Find four different solutions of the equation x + 2y = 6.

Solution :  Given  x + 2y = 6                      -----------(1)

By inspection, x = 2, y = 2 is a solution because for x = 2, y = 2

x + 2y = 2 + 4 = 6

Now, let  x = 0  sub in eqn(1)

We get   2y = 6

The unique solution y = 3. So x = 0, y = 3 is also a solution of x + 2y = 6.

Similarly, taking y = 0,

The given equation reduces to x = 6. So, x = 6, y = 0 is a solution of x + 2y = 6 as well.

 Finally, let us take y = 1. The given equation now reduces to

x + 2 = 6,

x=6-2

x = 4.

Therefore, (4, 1) is also a solution to the given equation.

So four of the infinitely many solutions of the given equation are: (2, 2), (0, 3), (6, 0) and (4, 1).

Graph of a Linear Equation in Two Variables

To draw the graph of linear equation in two variables, we need to draw a table to write the solutions of the given equation, and then plot them on the Cartesian plane. By joining these coordinates, we get the line of that equation. The coordinates which satisfy the given Equation lies on the line of the equation. Every point (x, y) on the line is the solution x = a, y = b of the given Equation. Any point, which does not lie on the line AB, is not a solution of Equation.

Example:

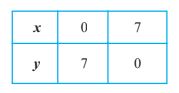
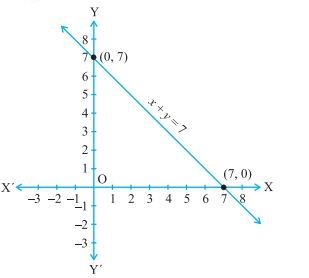
1.Draw the graph of x + y = 7.

Solution: To draw the graph, we need at least two solutions to the equation.

You can check that x = 0,y = 7, and x = 7, y = 0 are solutions of the given equation.

So, you can use the following table to draw the graph.

graph:

Equations of Lines Parallel to the x-axis and y-axis

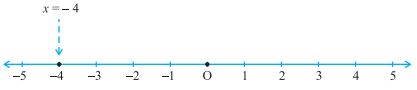
Q) Solve the equation 2x + 1 = x – 3, and represent the solution on

(i) The number line,

(ii) The Cartesian plane.

Solution:

We solve 2x + 1 = x – 3, to get

2x – x = –3 – 1

i.e., x = –4

(i) The representation of the solution on the number line is shown in Fig. where x = – 4 is treated as an equation in one variable.

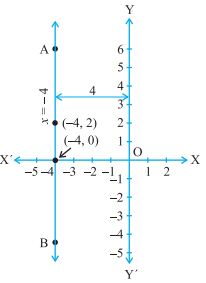
(ii) We know that x = – 4 can be written as x + 0.y = – 4
which is a linear equation in the variables x and y. This is represented by a line. Now all the values of y are permissible because 0. i.e;y=0

However, x must satisfy the equation x = – 4. Hence, two solutions of the given equation are x = – 4, y = 0 and x = – 4, y = 2.
The graph AB is a line parallel to the y-axis and at a distance of 4 units to the left of it.
Similarly, you can obtain a line parallel to the x-axis corresponding to equations of the type y = 3.