*/ ?>
  • Login
  • Register
    • Home SSC 9th Class MATHEMATICS
    */ ?>

    1.REAL NUMBERS12

    2.POLYNOMIALS AND FACTORISATION13

    3.THE ELEMENTS OF GEOMETRY3

    4. LINES AND ANGLES10

    5.CO-ORDINATE GEOMETRY 5

    6.LINEAR EQUATIONS IN TWO VARIABLES9

    7.TRIANGLES 10

    8.Quadrilaterals8

    9.Statistics5

    10.Surface areas and volumes9

    11.Areas5

    12.Circles6

    13.Constructions4

    14.Probability4

    15.Proofs in Mathematics8

    Basic Constructions

    Basic Constructions

     

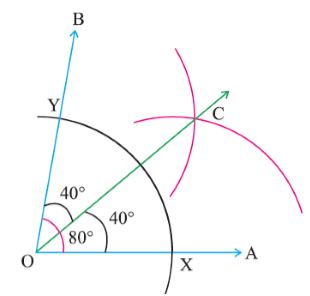
    Construct the bisector of an angle:

    If we have to bisect the ∠BOA, then we need to follow these steps to construct the bisector of the angle.

    Step 1: Take O as the center and draw an arc by any radius intersecting the rays OA and OB at X and Y respectively.

    Step 2: Now take X and Y as the center and Draw arcs that intersect each other at a point C with a radius more than (1/2) XY.

    Step 3: Join OC to draw a ray which is the required bisector of the ∠BOA.

    Example: ∠BOA = 80° and OC bisects it in ∠BOC and ∠COA which is 40° each.

     

                          

     

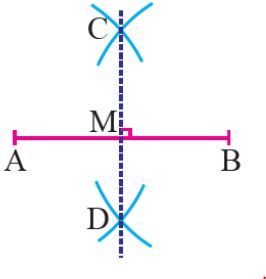
    Construct the perpendicular bisector of a given line segment:

    We have to bisect the given line segment AB.

    Step 1: Take A and B as the centers and radius more than 1/2 of Ab and draw the arcs on both sides. construct the perpendicular bisector of a given line segment.

    Step 2: These arcs should intersect each other at C and D. And join CD.

    Step 3: Here CD intersects AB at point M so that M is the midpoint of AB and CMD is the required perpendicular bisector of AB. Join A and B to both C and D to form AC, AD, BC, and BD.

     

                                   

     

    In triangles CAD and CBD,

    AC = BC (Arcs of equal radii)

    AD = BD (Arcs of equal radii)

    CD = CD (Common)

    Therefore,  CAD ≅ CBD (SSS rule)

    So, ∠ ACM = ∠ BCM (CPCT)

    Now in triangles CMA and CMB,

    AC = BC (As before)

    CM = CM (Common)

    ∠ ACM = ∠ BCM (Proved above)

    Therefore,  CMA ≅  CMB (SAS rule)

    So, AM = BM and ∠ CMA = ∠ CMB (CPCT)

    As ∠ CMA + ∠ CMB = 180° (Linear pair axiom),

    Now we get

    ∠ CMA = ∠CMB = 90°.

    Therefore, CMD is the perpendicular bisector of AB.

     

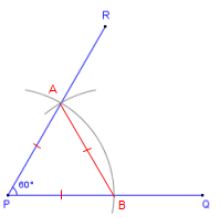
    Construct an angle of 60° at the initial point of a given ray:

    We have to draw an angle of 60° at the given point P.

    Step 1: Take P as the center and draw an arc of any radius which intersects PQ at point B.construct an angle of 60°

    Step 2: Now Take B as a center and draw an arc with the same radius as before which intersects the previous arc at point A.

    Step 3: Now draw a ray PR in which passé through Point A and the ∠RPQ is the required angle of 60°.Join AB.

    Then, AP = AB = PB (By construction)

    Therefore,? ABP is an equilateral triangle and the ∠ APB, which is the same as ∠ RPQ is equal to 60°.

                               

     

    © - 2018 KlassPM Educational Consultancy Pvt Ltd. All Rights Reserved.