Constructions of Triangles

Construct a triangle if its base, a base angle, and some of the other two sides are given :

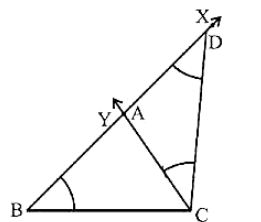
Given the base BC, a base angle ∠B and the sum of other two sides AB + AC of a triangle ABC, now we need to construct it.

Construction of TrianglesSteps of Construction:

Step 1: First of all, draw the base BC and at point B make an∠XBC equal to the given angle.

Step 2: From the ray BX, cut the line segment BD = AB + AC.

Step 3: Join DC now which makes ∠DCY = ∠BDC.

Step 4: When CY intersects BX at A then it forms the required triangle i.e. ABC.   

Construct a triangle if its base, a base angle and the difference of the other two sides are given:

Given the base BC, a base angle i.e. ∠B and the difference of the other two sides AB – AC or AC – AB, we need to construct the triangle ABC. There could be two cases:

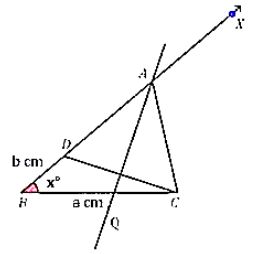
Case (i): If AB > AC that is AB – AC is given.

construct a triangleSteps of Construction:

Step 1: Draw the base BC which is equal to a cm and at the point, B makes an∠XBC = x°.

Step 2: From ray, BX cut the line segment BD which is equal to AB–AC.

Step 3: Join DC and draw the perpendicular bisector of DC.

Step 4: This perpendicular bisector intersects BX at a point A.

             By joining A to C we get the required triangle i.e. ABC.

Case (ii): If AB < AC that is AC – AB is given.

Steps of Construction:

required triangle ABC

Step 1: Draw the base BC and at point B make an ∠XBC.

Step 2: From ray, BX cut the line segment BD which is equal to AC – AB from the line BX by extending it on the opposite side of line segment BC.

Step 3: Join DC and draw the perpendicular bisector of DC.

Step 4: Let PQ intersect BX at A and by joining A to C, we get the required triangle ABC.

Construct a triangle if its perimeter and two base angles are given:

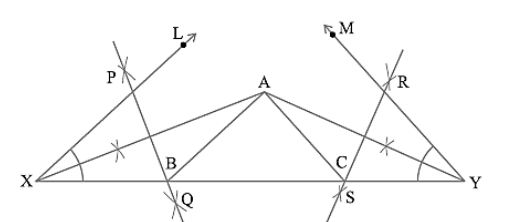
Given the base angles, say ∠ B and ∠ C and BC + CA + AB, you have to construct the triangle ABC.

Steps of Construction:

Step 1: Draw a line segment XY = BC + CA + AB.

Step 2: Make ∠LXY = ∠B and ∠MYX = ∠C.

Step 3: Now bisect ∠ LXY and ∠ MYX. These bisectors will intersect at a point A.

Step 4: Draw perpendicular bisectors PQ of AX and RS of AY.

Step 5: Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC.

Then ABC is the required triangle.